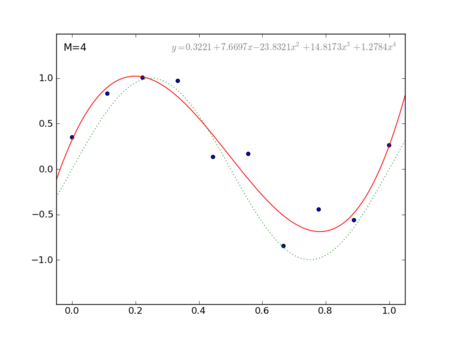
§1.1「例：多項式曲線フィッティング」

• データは にgaussian noise()を加えて人工的に作った10点（※PRMLと同じデータを使用）
• これを多項式 で近似
• 二乗和誤差 を最小化するを求める
• 次元数Mをいろいろ変えてover-fittingしていく様子を楽しむ
• Pythonで書いたらどんな感じかな？って試してみてるだけなんだからね
• てかpylabかわいいよpylab

curvefitting.txt

0.000000 0.349486
0.111111 0.830839
0.222222 1.007332
0.333333 0.971507
0.444444 0.133066
0.555556 0.166823
0.666667 -0.848307
0.777778 -0.445686
0.888889 -0.563567
1.000000 0.261502

curvefitting.py

# -*- coding: utf-8 -*-

from pylab import *
#from numpy import *

# PRMLと同じデータを読み込む
D = loadtxt("./curvefitting.txt")
x = D[:,0]
t = D[:,1]

# 自分でデータを作るならこんな感じ
# N = 10
# x = linspace(0.0, 1.0, N)
# t = sin(2*pi*x) + randn(N)*0.3 # with Gaussian noise of variance 0.09

# E(w)を最小にするwを求める。演習1.1参照
def fitting1(x,t,M):
  A = zeros((M+1,M+1))
  T = zeros(M+1)
  for i in xrange(M+1):
    T[i] = sum(t*map(lambda _:_**i, x))
    for j in xrange(M+1):
      A[i,j] = sum(map(lambda _:_**(i+j), x))
  return solve(A,T)

# ちょっと計算量を減らした
def fitting(x,t,M):
  A = zeros((M+1,M+1))
  T = zeros(M+1)
  xi = [ones(len(x))]
  si = [len(x)]
  for i in xrange(M*2):
    xi.append(xi[i] * x)
    si.append(sum(xi[i+1]))
  for i in xrange(M+1):
    T[i] = sum(t*xi[i])
    for j in xrange(M+1):
      A[i,j] = si[i+j]
  return solve(A,T)

# y(x,w)
def make_y(w,M):
  return lambda x: sum(w*map(lambda _:x**_, xrange(M+1)))

# y(x,w) をTeX表記に展開
def make_text(w,M):
  def ftos(x):
    return '%.4f' % x
  def xi(i):
    if i == 1:
      return 'x'
    else:
      return 'x^{' + str(i) + '}'
  coeffs = ['y=' + ftos(w[0])]
  for i in xrange(1,M+1):
    if w[i] < 0:
      coeffs.append('-' + ftos(-w[i]) + xi(i))
    else:
      coeffs.append('+' + ftos(w[i]) + xi(i))
  texts = []
  for ar in split(coeffs, [5,8,11,14]):
    texts.append(r'$\it{' + ''.join(ar) + '}$')
  return texts


for M in xrange(0,16):
  w = fitting(x,t,M)
  y = make_y(w,M)
  tex = make_text(w,M)

  gx = linspace(-0.05, 1.05, 100)
  gy = amap(y, gx)

  axis([-0.05, 1.05, -1.49, 1.49])
  scatter(x, t)
  plot(gx, gy, 'r-', lw=1)
  plot(gx, sin(2*pi*gx), 'g:', lw=1)
  ty = 1.3
  text(-0.025, ty, 'M='+str(M), fontsize=13, horizontalalignment='left')
  for tex in make_text(w,M):
    text(1.025, ty, tex, color='gray', fontsize=12, horizontalalignment='right')
    ty -= 0.11
  savefig("curvefitting_%d" % M)
  clf()