Google Code Jam 2019 - Qualification Round

4/6(土)08:00 - 4/7(日)11:00
Qualに限って相談OKなので、有志4人で集まって電源wifi完備なカラオケルームを借りて参加*1

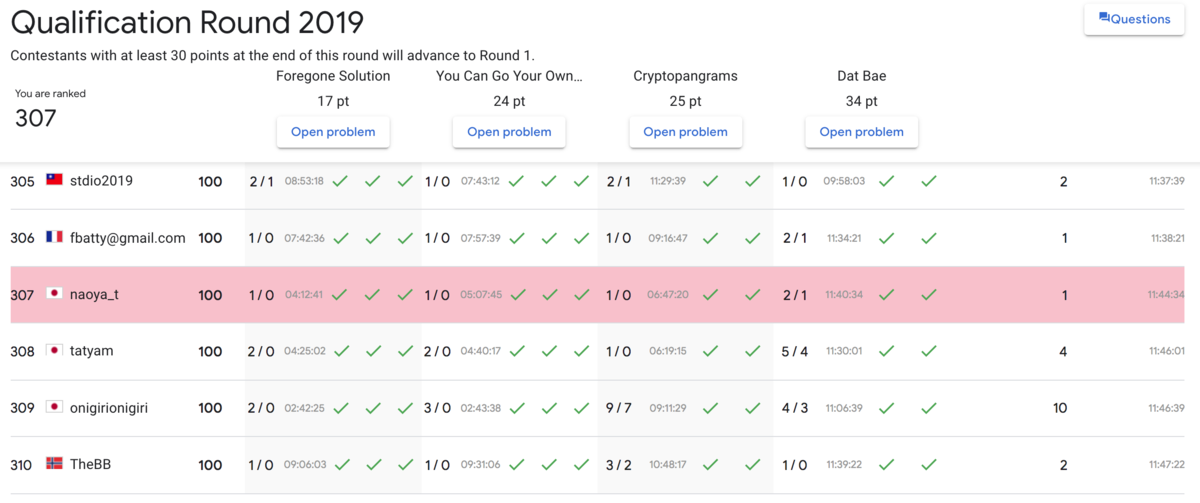
全員予選通過ライン（30点）は超えられたので目的は果たせたかと

会場でD-smallまで解いて（提出は帰宅後）
その後D-largeも解いて終了。

終了後ジャッジでLargeも全て通って100点満点

次はRound 1でお会いしましょう。

【参考資料】当日のセットリスト（誰がどれを歌ったかは秘匿）
docs.google.com

A - Foregone Solution (6 + 10 + 1)

• Largeがとか言ってるので
• 数値としてではなく文字列として読み込んで、桁ごとにAとBに分解する感じで構築
• k=4の桁は3+1、それ以外はk+0で
• （必ず4が一度は含まれるので小さい方も0になることはない）

→AC(s1,s2; L)

void solve(string& s){
    int L = s.size();
    stringstream ss1, ss2;
    bool stand = false;
    rep(i,L){
        int n = s[i] - '0', a = n, b = 0;
        if (a == 4) { a = 3; b = 1; }
        ss1 << a;
        if (b) stand = true;
        if (stand) {
            ss2 << b;
        }
    }
    if (!stand) ss2 << 0;
    cout << ss1.str() << " " << ss2.str() << endl;
}

int main() {
    int N; cin >> N;
    rep1(z,N) {
        string s; cin >> s;
        printf("Case #%d: ", z);
        solve(s);
    }
    return 0;
}

B - You Can Go Your Own Way (5 + 9 + 10)

• EをSに、SをEに置換すれば対角線＼でフリップした感じに出来るのでは
• ある点にたどり着く方法はいくつもあるが、手数は一定なので鏡像が同じ道をたどることはありえない

→AC(s1,s2; L)

void solve(int N, string& s) {
    int L = s.size();
    rep(i,L){
        switch (s[i]) {
            case 'S': putchar('E'); break;
            case 'E': putchar('S'); break;
            default: break;
        }
    }
    putchar('\n');
}

int main() {
    int T; cin >> T;
    rep1(z,T){
        int N; cin >> N;
        string s; cin >> s;
        printf("Case #%d: ", z);
        solve(N, s);
    }
    return 0;
}

C - Cryptopangrams (10 + 15)

• 高々100個の数を総当たりでgcd
  • big integerを使いたいのでpythonで
• 共通の素数を持っていればgcd≠1になるので、それを利用して2つの素数の積に分解できる
  • 出現する素数（26個あるはず）を昇順に並べ替え、小さい方からそれぞれA〜Zとする
• 暗号文は2つの素数のペアのリストになるので、
  • 最初のペアのどちらを左端にしたら辻褄が合うか（両方やってみる）
• で文字列を再構築

→AC(s; L)

# -*- encoding: utf-8 -*-
import sys
from fractions import gcd  # python<=3.4

def sub(pairs, start):
    L = len(pairs)
    ans = [start]
    for a, b in pairs:
        if a == start:
            next = b
        elif b == start:
            next = a
        else:
            return None
        ans.append(next)
        start = next
    return ans

def solve(N,L,s):
    assert L == len(s)
    tmp = set()
    for i in range(L-1):
        for j in range(i+1, L):
            if s[i] == s[j]:
                continue
            g = gcd(s[i], s[j])
            if g == 1:
                continue
            a = s[i] / g
            b = s[j] / g
            tmp.add(g)
            if a > 1:
                tmp.add(a)
            if b > 1:
                tmp.add(b)

    primes = sorted(list(tmp))

    dct = { n: chr(0x41+i) for i,n in enumerate(primes) }

    pairs = []
    for n in s:
        for p in primes:
            if n % p == 0:
                q = n / p
                pairs.append((p,q))
                break
            else:
                continue
    assert len(s) == len(pairs)
    m0 = sub(pairs, pairs[0][0])
    m1 = sub(pairs, pairs[0][1])
    msg = m0 or m1
    return ''.join([dct[p] for p in msg])

T = int(raw_input())
for i in range(T):
    N, L = map(int, raw_input().rstrip().split())
    s = map(long, raw_input().rstrip().split())
    print 'Case #%d: %s' % (1+i, solve(N,L,s))

D - Dat bae (14 + 20)

F=10の場合

• 10回使って、子機それぞれが0〜1023を示すようにする
• 10回の返答を0〜1023の数に変換し、出現しなかった数を答える

とりあえずF=5のときは嘘解答を投げるようにして
→AC(s; L)

vi solve10(int N, int B, int F) {
    assert(F >= 10);

    int R = N - B;
    vi alive(R, 0);
    for (int i=0; i<10; ++i) {
        rep(p,N) {
            // m[p] = (p & b) ? 1 : 0;
            int bit = (p >> i) & 1;
            putchar('0' + bit);
        }
        putchar('\n');
        fflush(stdout);

        string res; cin >> res;
        assert(res.size() == R);
        rep(j,R) {
            alive[j] |= ((res[j] - '0') << i);
        }
    }
    set<int> alive_set(ALL(alive));
    vi ans;
    rep(i,N) {
        if (!found(alive_set, i)) ans.pb(i);
    }
    return move(ans);
}

vi solve5(int N, int B, int F) {
    // uso
    rep(i,F){
        rep(p,N){
            putchar('0');
        }
        putchar('\n');
        fflush(stdout);

        string res; cin >> res;
        assert(res.size() == R);
    }

    vi ans(B);
    rep(i,B) ans[i] = i;
    return move(ans);
}

int main() {
    int T; cin >> T;
    rep(z,T){
        int N,B,F; cin >> N >> B >> F;
        vi ans;
        if (F >= 10) {
            ans = solve10(N,B,F);
        } else {
            ans = solve5(N,B,F);
        }
        assert(ans.size() == B);
        rep(i,B) {
            printf("%d%c", ans[i], (i==B-1)?'\n':' ');
            fflush(stdout);
        }
        int verdict; cin >> verdict;
        if (verdict == -1) break;
    }
    return 0;
}

帰宅後

F=5の場合

• 5回使って、子機それぞれが0〜31を示すようにする（というか0〜31しか作れない）
  • 0 1 2 3 ... 29 30 31 0 1 2 3 ... 29 30 31 0 1 2 3 ... のようになる
• 5回の返答を0〜31の数に変換し、出現しなかった数を答える

→先日のyukicoderエイプリルフールコンテストのF問題「怪文書」の方式

• • 出現しない個数は高々15個なので、どこが欠けてるか知ることができそう

→AC(s1)

vi solve5(int N, int B, int F) {
    assert(F >= 5);

    int R = N - B;
    vi alive(R, 0);
    for (int i=0; i<5; ++i) {
        rep(p,N) {
            int pid = p % 32;
            int bit = (pid >> i) & 1;
            putchar('0' + bit);
        }
        putchar('\n');
        fflush(stdout);

        string res; cin >> res;
        assert(res.size() == R);
        rep(j,R) {
            alive[j] |= ((res[j] - '0') << i);
        }
    }

    int ofs = 0;
    rep1(i,R-1) {
        alive[i] += ofs;
        if (alive[i] < alive[i-1]) {
            ofs += 32;
            alive[i] += 32;
        }
    }

    set<int> alive_set(ALL(alive));
    vi ans;
    rep(i,N) {
        if (!found(alive_set, i)) ans.pb(i);
    }

    return move(ans);
}

int main() {
    int T; cin >> T;
    rep(z,T){
        int N,B,F; cin >> N >> B >> F;

        vi ans = solve5(N,B,F);
        assert(ans.size() == B);
        rep(i,B) {
            printf("%d%c", ans[i], (i==B-1)?'\n':' ');
            fflush(stdout);
        }
        int verdict; cin >> verdict;
        if (verdict == -1) break;
    }
    return 0;
}

F=4でも行けるという話ですね

*1:1AC→1曲歌ったら次の問題に進める