Pythonで数値積分 〜フーリエ級数展開を例に、てかscipy.integrate.quad()かわいいよscipy.integrate.quad()

はいはいまたグラフ描きたいだけのエントリですよ。てか数値積分が簡単に出来ちゃうSciPy(・∀・)ｲｲﾈ!!

が

from scipy.integrate import quad

y, abserr = quad(f, a, b)

で計算できちゃうのです。（y が積分値、abserrは推定誤差の絶対値）

基礎編

→ を期待。

# -*- coding: utf-8 -*-
from scipy.integrate import quad

y, abserr = quad(lambda x:x*x*x, 0, 2)
print "∫_0^2 x^3 dx = %g ± %g" % (y, abserr)

→ ∫_0^2 x^3 dx = 4 ± 4.44089e-14
正解。推定誤差も小さい。
相手はSciPy様なので人間に正解とか言われてもおそらくあれですね。

→ を期待。

# -*- coding: utf-8 -*-
from numpy import sin
from scipy.integrate import quad

y, abserr = quad(sin, 0, pi/3)
print "∫_0^{¥pi/3} sin x dx = %g ± %g" % (y, abserr)

→ ∫_0^{\pi/3} sin x dx = 0.5 ± 5.55112e-15
これも正解。

応用編

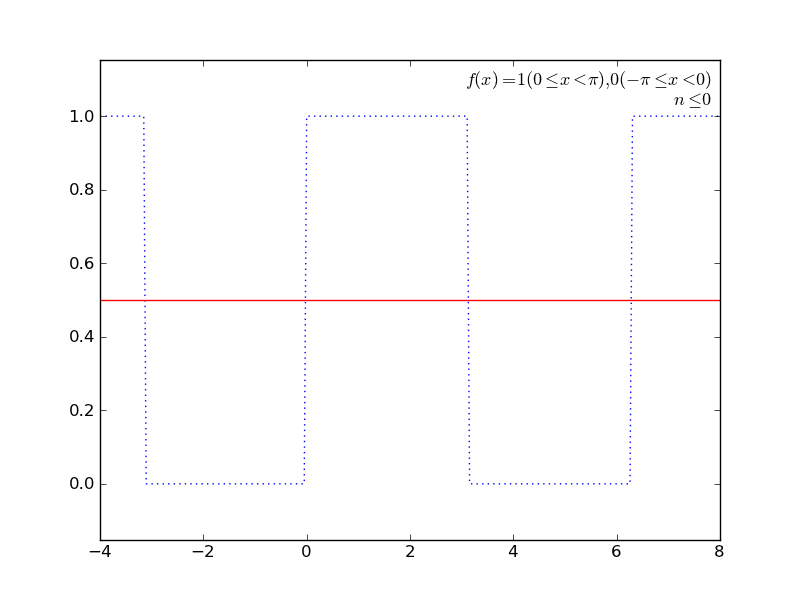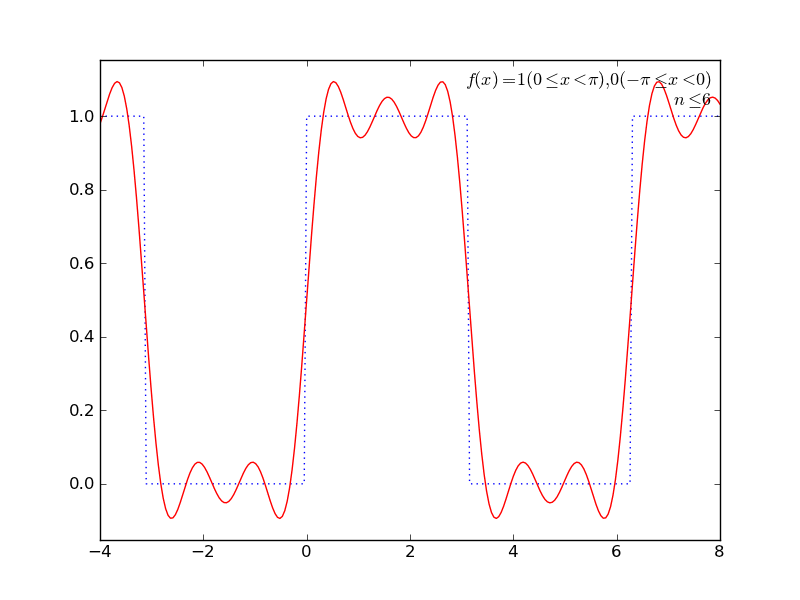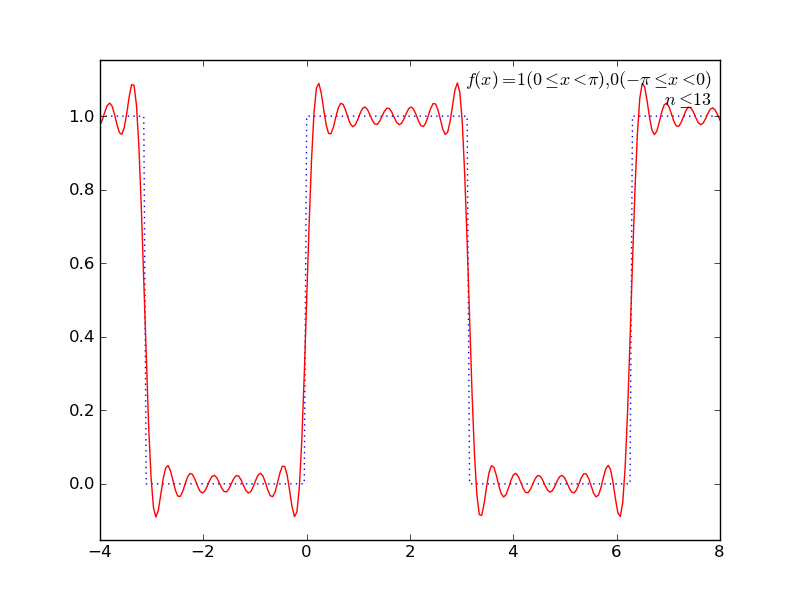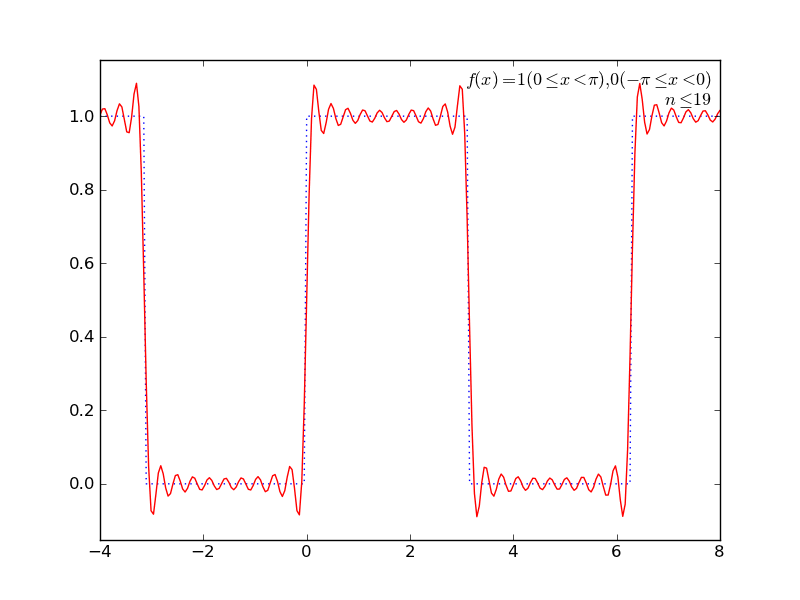
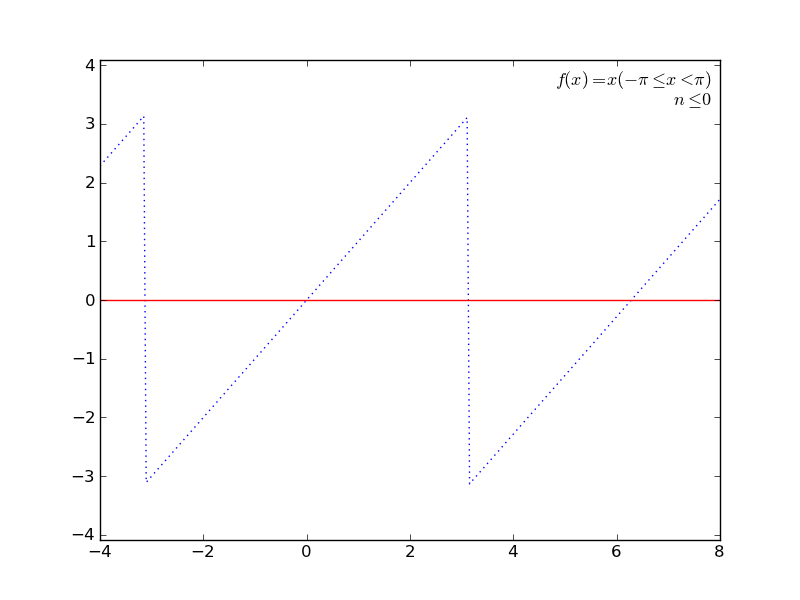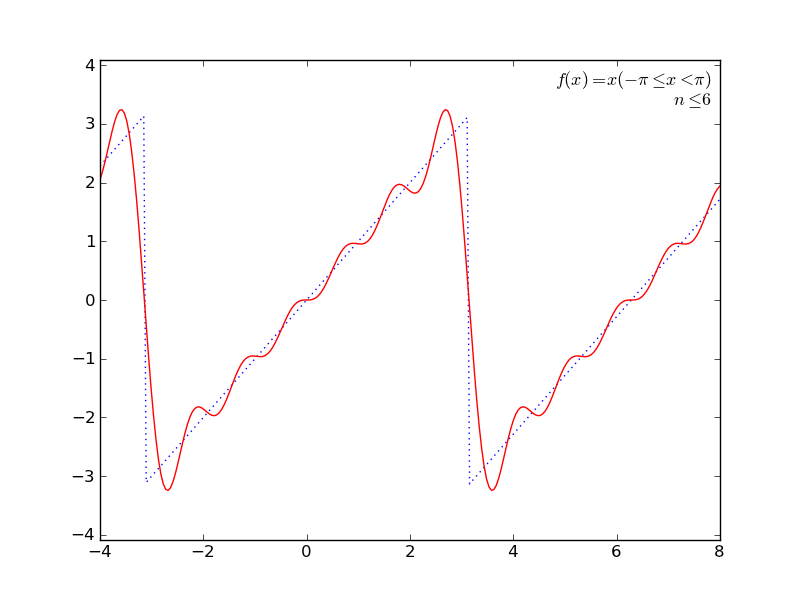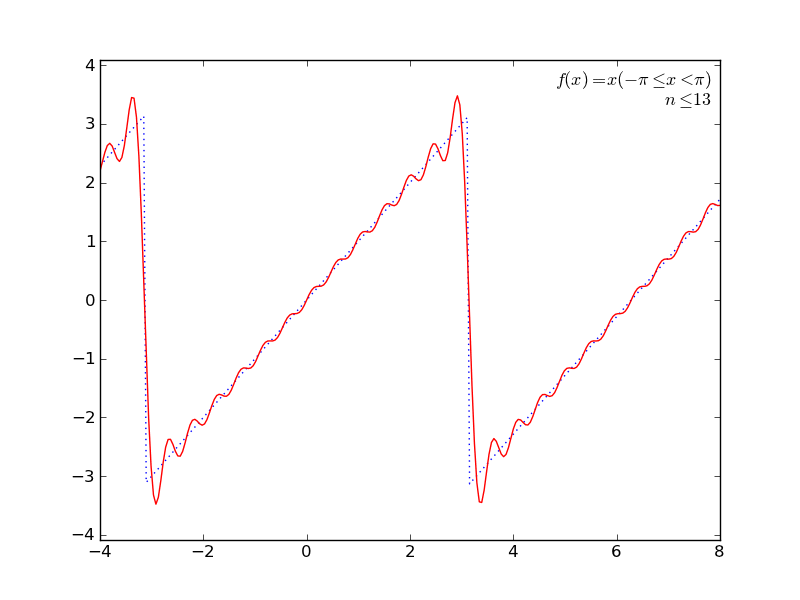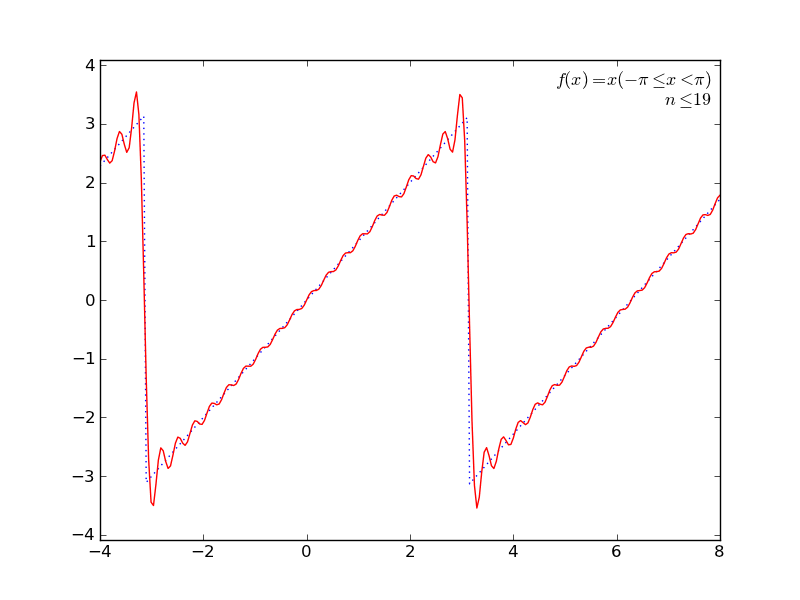
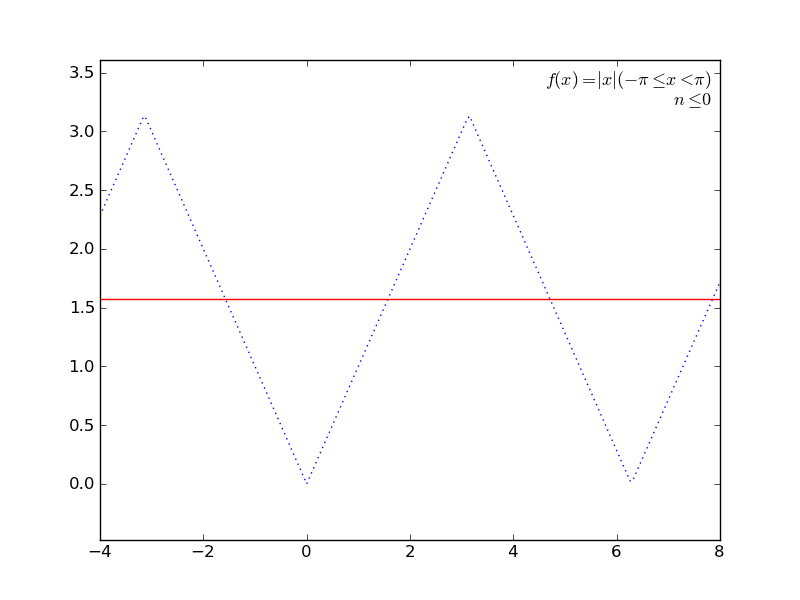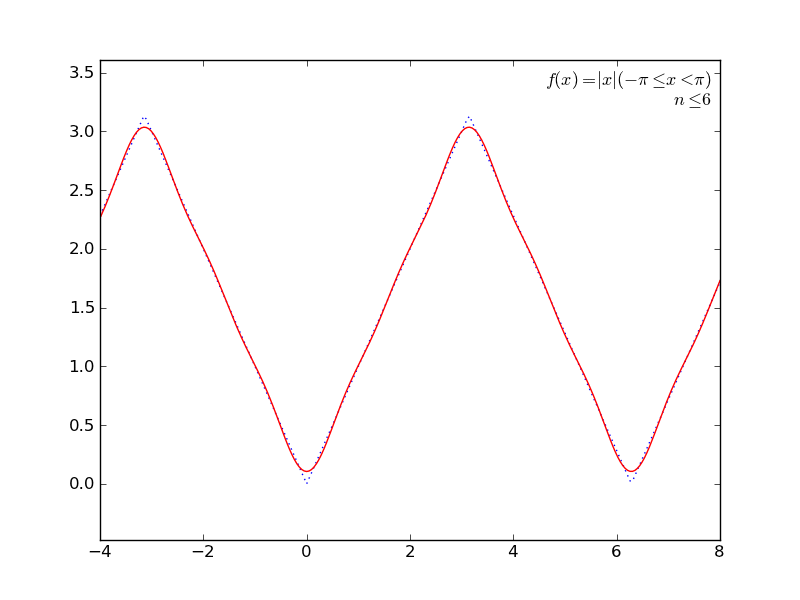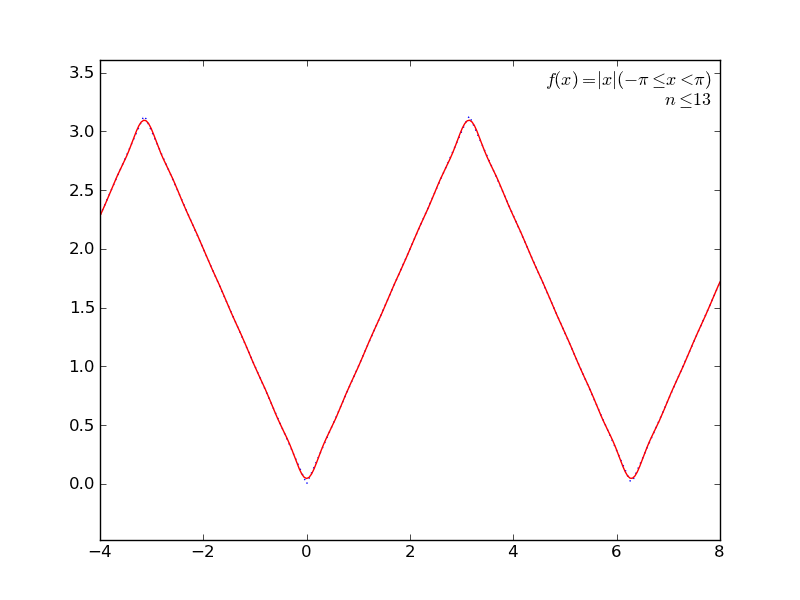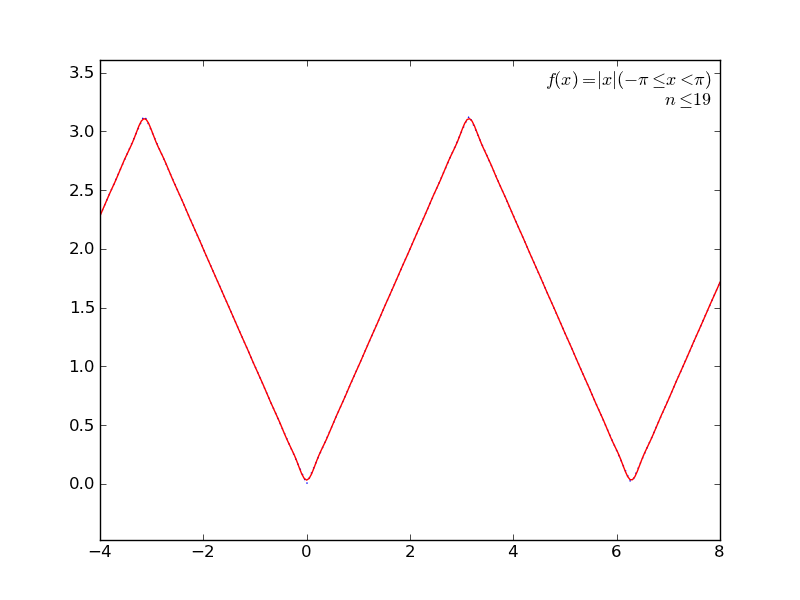
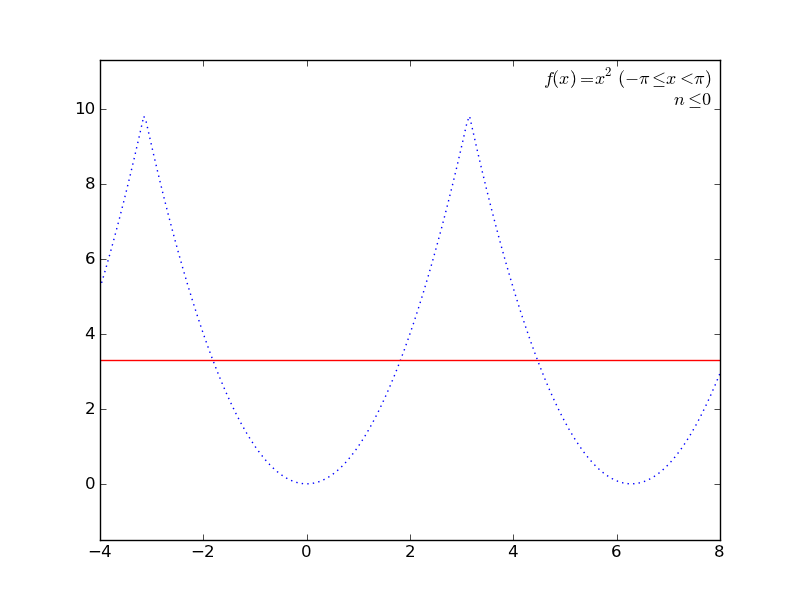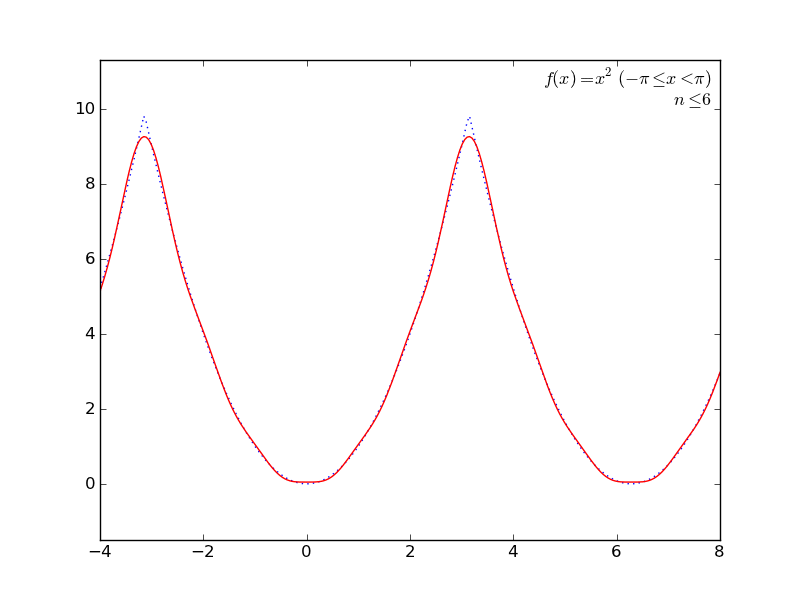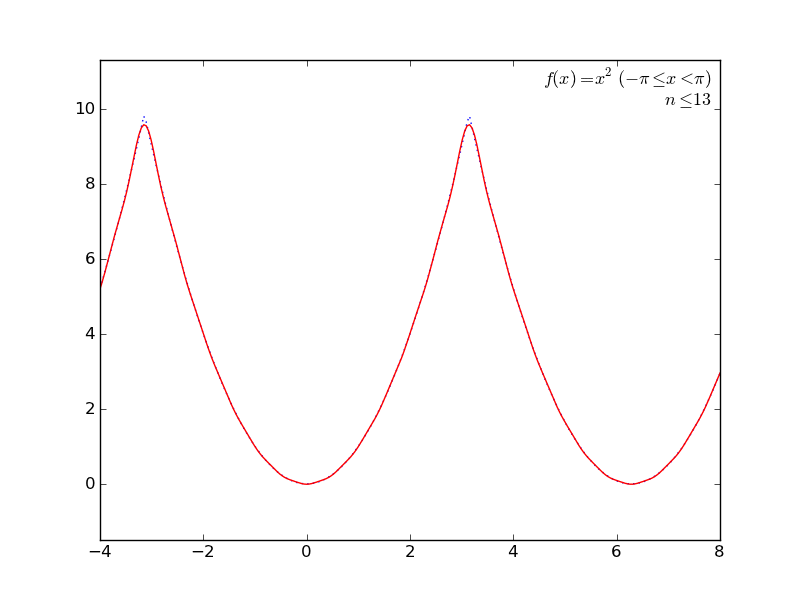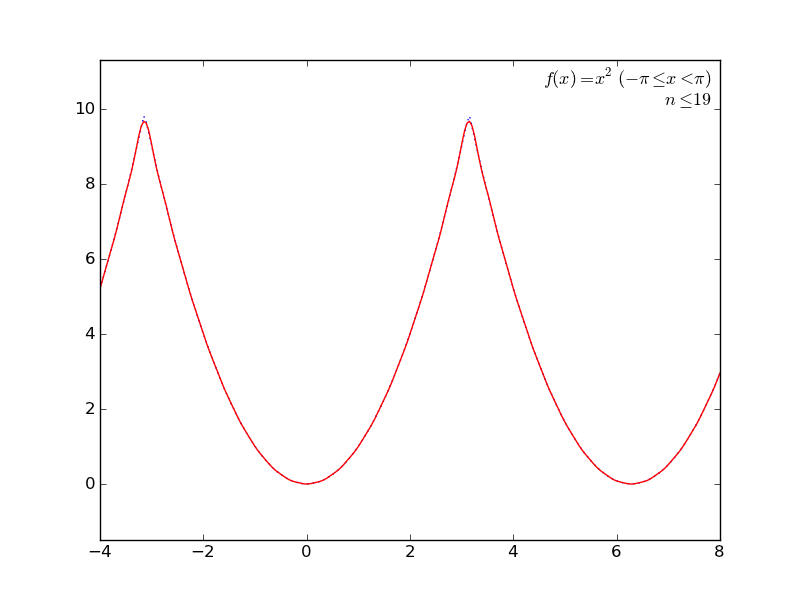
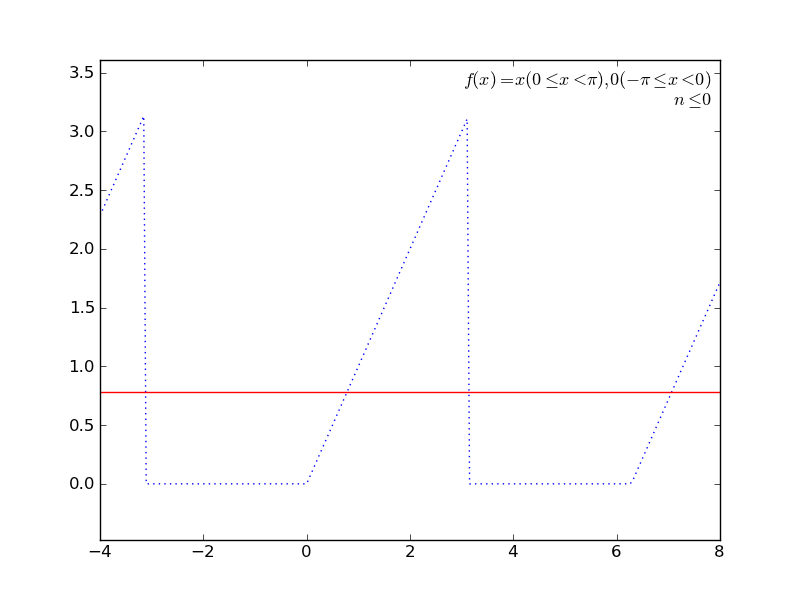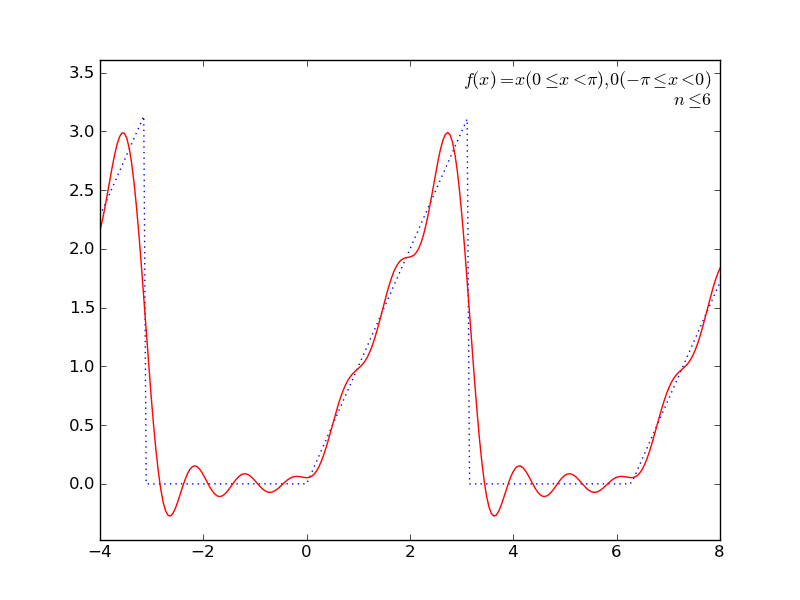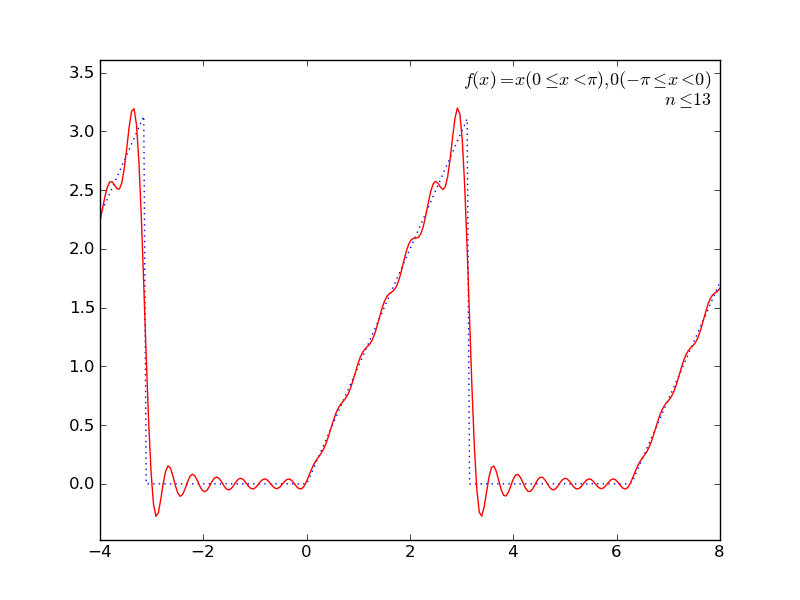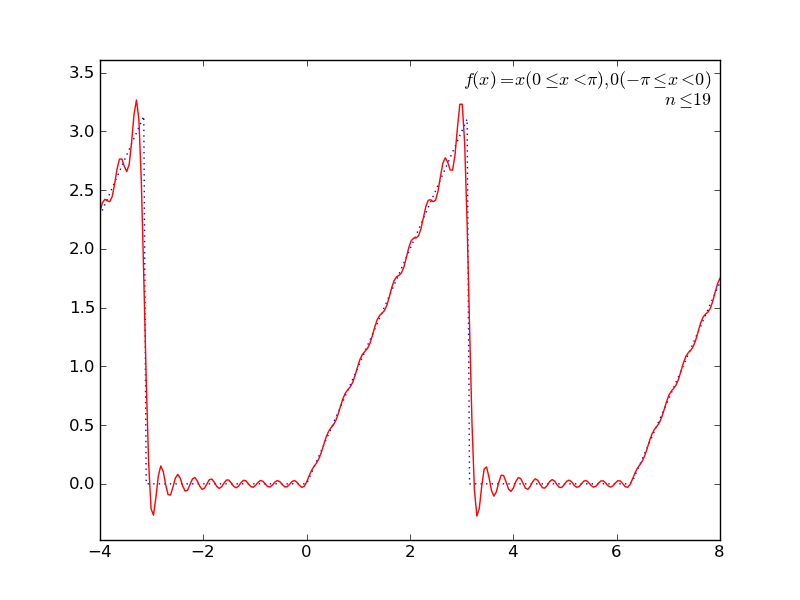
定積分を使ってて簡単そうなところで（かつグラフが描けそうなところで←ここ重要）、フーリエ級数展開とかしてみる。

の係数の計算に定積分を使うあれです。

• 
• 

# -*- coding: utf-8 -*-
from pylab import *
from scipy.integrate import quad

def fourier(fun, n_max):
  a = []
  b = []
  for n in xrange(0, 1+n_max):
    res, err = quad(lambda x:fun(x)*cos(n*x), -pi, pi)
    a.append(res/pi)
    res, err = quad(lambda x:fun(x)*sin(n*x), -pi, pi)
    b.append(res/pi)
  def fn(x):
    sum = a[0] / 2
    for n in xrange(1, 1+n_max):
      sum += a[n]*cos(n*x) + b[n]*sin(n*x)
    return sum
  return fn

def f(x):
  x = (x + pi) % (pi * 2) - pi
  if x >= 0:
    return 1
  else:
    return 0

x_min = -pi - 0.5
x_max = pi*2 + 0.5
y_min = -0.25
y_max = 1.25
axis([x_min, x_max, y_min, y_max])

f_fn = fourier(f, 10)
xs = linspace(x_min, x_max, 256)
plot(xs, amap(f, xs), 'b:', lw=1)
plot(xs, amap(f_fn, xs), 'r-', lw=1)
show()

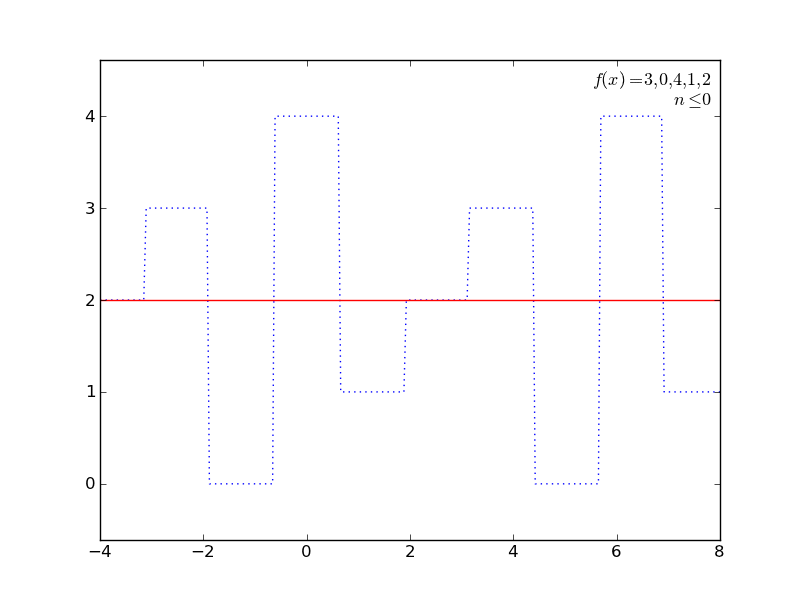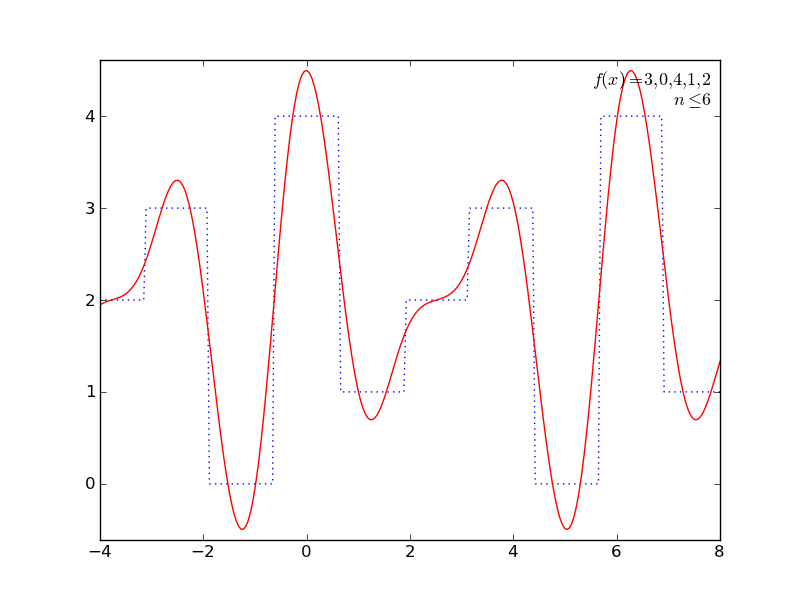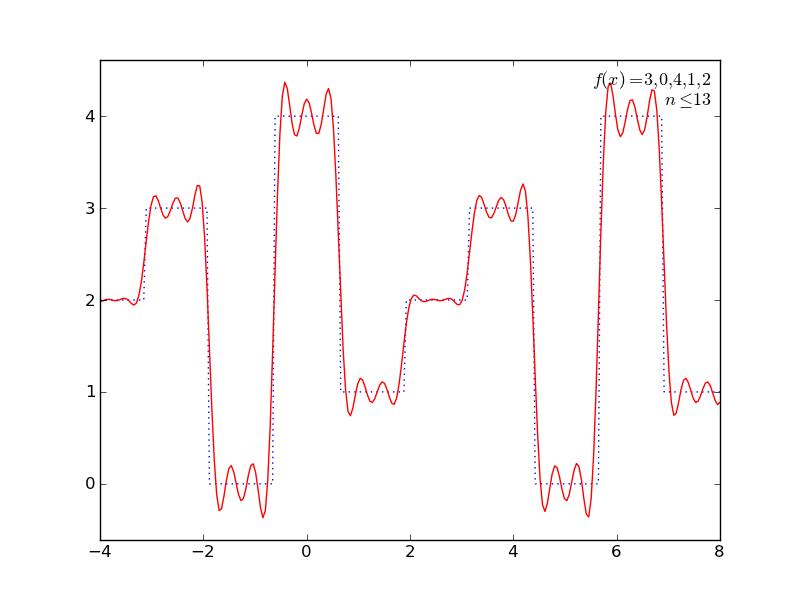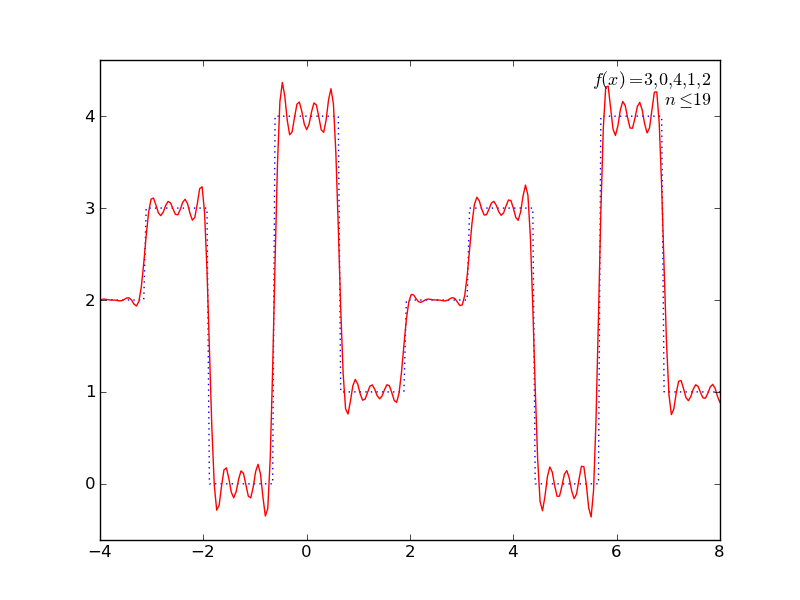
いくつか遊んでみた結果をアニメGIFにしてみた。ImageMagickで

$ convert -delay 42 f1_*.png -loop 0 anime_f1.gif

みたいに。

Gistに貼ったソースをここにembedしてみるテスト。（2/27から出来るようになったらしいので）
ライセンスはNYSLでどぞ。