三分探索と黄金分割探索

はい、毎度おなじみのグラフ描きたいだけのエントリですw

今回のお題は「三分探索（ternary search）」。

二分探索（binary search）は割とおなじみかと思うのですが、二分探索が単調増加(減少)関数fについてf(x)=kとなるxを求めるのに対し、三分探索（とか黄金分割探索）は凸関数の極値を求めるのに用います。

詳しくは

• http://d.hatena.ne.jp/ir5/20090630/1246349028
• http://d.hatena.ne.jp/nodchip/20090303/1236058357

辺りを見て頂くとして。

三分探索

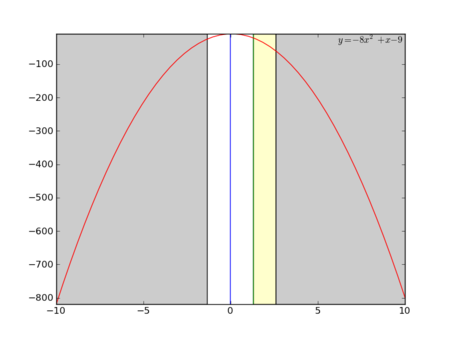
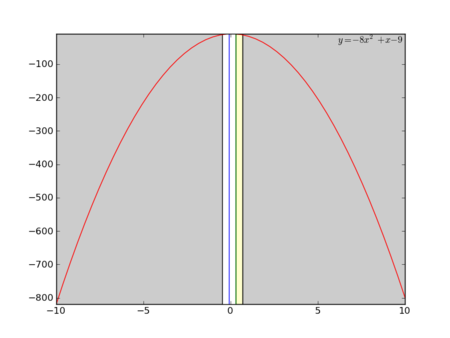
1. 探索領域(x0,x3)を三等分するx1,x2を選びます。(x0,x1,x2,x3)
2. で、f(x1)とf(x2)を比べ、f(x)が下に凸な関数なら値が大きい方、上に凸な関数なら値が小さい方の外側（x1ならx0-x1, x2ならx2-x3）を捨てます。
3. 気が済むまで続けます。

黄金分割探索

1. 三等分ではなく、黄金比を使い探索領域を 1:φ, φ:1 にそれぞれ分割するx1,x2 を選びます。です。
2. あとは三分探索と同様なのですが、
3. 黄金比なので捨てずに残った分割位置と値が次のステップで流用できる点（←何でそうなるのかはちょっと計算したらわかります）、あと捨てる比率が多めなので収束が速めな点が黄金分割探索のメリット

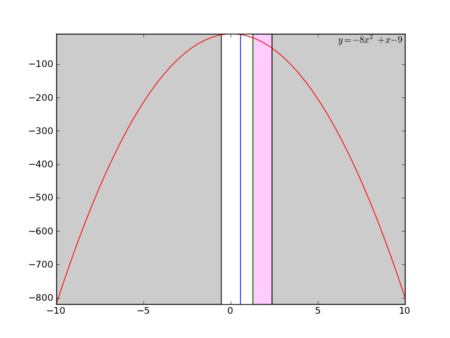
黄金分割探索の方がちょっと収束が速めなのが見て取れる・・・ような

コード

pylabの練習のためにPythonで書いてます。

# -*- coding: utf-8 -*-

import random
from pylab import *

f = lambda x:-8*x**2+x-9
txt = 'y=-8x^2+x-9'
ymax = f(1.0/16) # y'=-16x+1=0 ∴argmax=1/16

lo0 = -10.0
hi0 = 10.0
e = 1.0 # 探索打ち切り精度。グラフ的にこの辺りまでしか見えないから1.0だけど普通は1e-6とか1e-9とかじゃないかな
ymin = min(f(lo0),f(hi0))

## 三分探索
lo = lo0
hi = hi0

z = 0
while lo + e < hi:
  clf()
  z += 1

  x1 = (lo*2 + hi) / 3
  x2 = (lo + hi*2) / 3
  y1 = f(x1)
  y2 = f(x2)

  axis([lo0,hi0, ymin,ymax])

  # lines
  plot([x1,x1],[ymin,ymax])
  plot([x2,x2],[ymin,ymax])

  t = linspace(lo0, hi0)
  text(9.9, ymax,'$'+txt+'$', horizontalalignment='right', verticalalignment='top')
  plot(t,map(f,t))
  
  if lo0 < lo:
    rect = matplotlib.patches.Rectangle((lo0,ymin),lo-lo0,ymax-ymin,facecolor="#cccccc")
    gca().add_patch(rect)
  if hi < hi0:
    rect = matplotlib.patches.Rectangle((hi,ymin),hi0-hi,ymax-ymin,facecolor="#cccccc")
    gca().add_patch(rect)

  if y1 < y2:
    rect = matplotlib.patches.Rectangle((lo,ymin), x1-lo,ymax-ymin, facecolor="#ffffcc")
    gca().add_patch(rect)
    lo = x1
  else:
    rect = matplotlib.patches.Rectangle((x2,ymin), hi-x2,ymax-ymin, facecolor="#ffffcc")
    gca().add_patch(rect)
    hi = x2

  show()

## 黄金分割探索
lo = lo0
hi = hi0

phi = (1.0 + sqrt(5)) / 2

z = 0
while lo + e < hi:
  clf()
  z += 1

  x1 = (lo*phi + hi) / (1.0+phi)
  x2 = (lo + hi*phi) / (1.0+phi)
  y1 = f(x1)
  y2 = f(x2)

  axis([lo0,hi0, ymin,ymax])

  # lines
  plot([x1,x1],[ymin,ymax])
  plot([x2,x2],[ymin,ymax])

  t = linspace(lo0, hi0)
  text(9.9, ymax,'$'+txt+'$', horizontalalignment='right', verticalalignment='top')
  plot(t,map(f,t))
  
  if lo0 < lo:
    rect = matplotlib.patches.Rectangle((lo0,ymin),lo-lo0,ymax-ymin,facecolor="#cccccc")
    gca().add_patch(rect)
  if hi < hi0:
    rect = matplotlib.patches.Rectangle((hi,ymin),hi0-hi,ymax-ymin,facecolor="#cccccc")
    gca().add_patch(rect)

  if y1 < y2:
    rect = matplotlib.patches.Rectangle((lo,ymin), x1-lo,ymax-ymin, facecolor="#ffccff")
    gca().add_patch(rect)
    lo = x1
    x1 = x2
    x2 = (lo + hi*phi)/(1.0+phi)
  else:
    rect = matplotlib.patches.Rectangle((x2,ymin), hi-x2,ymax-ymin, facecolor="#ffccff")
    gca().add_patch(rect)
    hi = x2
    x2 = x1
    x1 = (lo*phi + hi)/(1.0+phi)

  show()

おまけ

今回の件の本質ではないので上のコードでは数式決め打ちに見せかけていますが、xの２次式は実際にはランダムに毎回生成して遊んでいました。

## 多項式の係数の配列から、式をTeX表現したテキストを生成
def ftxt(a):
  dim = len(a)-1
  if dim < 0:
    return ""

  txt = ""
  pre = False
  for i in xrange(dim+1):
    if a[dim-i] == 0:
      continue

    if a[dim-i] < 0:
      txt += '-'
    elif pre:
      txt += '+'

    d = dim - i

    if d==0 or abs(a[dim-i]) != 1:
      txt += str(abs(a[dim-i]))

    if d >= 2:
      txt += 'x^' + str(d)
    elif d == 1:
      txt += 'x'

    pre = True

  return txt

## 多項式の係数の配列から、その多項式を微分した結果の多項式の係数の配列を計算して返す
def deriv(a):
  return [(i+1)*a[i+1] for i in xrange(len(a)-1)] if len(a)>1 else [0]

## 多項式の係数の配列から argmax を計算。手抜きして2次式にしか対応してないけど。
def argmax(a):
  dim = len(a)-1
  if dim == 2:
    de = deriv(a)
    return -1.0*de[0]/de[1]
  else:
    return 0

## 多項式の係数の配列から、実際に計算ができるlambda式を生成
def fgen(a):
  return lambda x:sum([a[i]*x**i for i in xrange(len(a))])

a = [random.randint(-9,9), random.randint(-9,9), random.randint(-9,-1)]
f = fgen(a)
txt = 'y='+ftxt(a)
xmax = argmax(a)
ymax = f(xmax)