Coursera: Robotics: 1. Aerial Robotics〈修了〉

全6部から成るCourseraのRobotics特別講座

Aerial Robotics
Computational Motion Planning
Mobility
Perception
Estimation and Learning
Capstone

の第1講 Aerial Robotics（4週間コース）を受講しました。ドローンに関する講座です。
f:id:n4_t:20180508220849j:plain

ドローンは安全性の問題や法整備など課題は多いし実社会での応用はまだまだこれからなのかなと思いますが、物流・農業・建築・災害救助をはじめ様々な分野での活用が期待されています。未来を感じます。

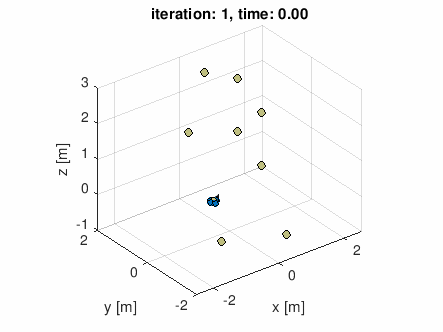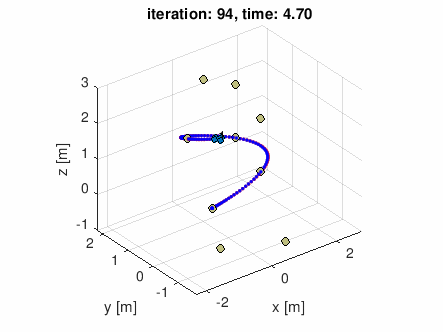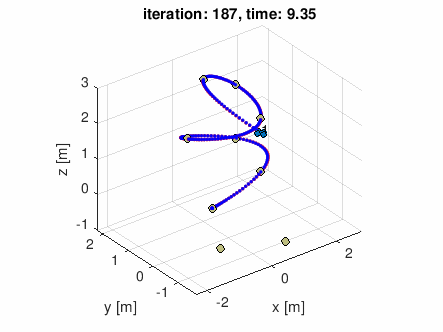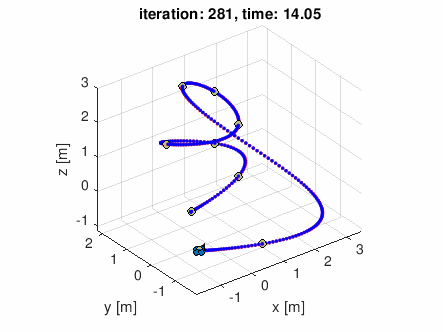
この講座では、クワッドローター（推進に4つの回転翼を用いるドローン）の飛行を制御するのに必要な物理学（力学）が学べます。最終週の課題では、空中の与えられた経由点のリストから飛行コースを計画し、計画した軌道に沿った飛行に必要な推力やモーメントの計算を行うプログラムを実装します。*1
f:id:n4_t:20180508133512g:plain

プログラミング実習ではMATLAB *2を使います。Webで使えるアカウントが1ヶ月無料でもらえる*3のでそれを使います。

講義は全編英語で行われています。（英語字幕可、日本語字幕はいまのところ無し）
先生の英語は若干訛りがあるけれどゆっくり目に話してくれているように思いますし、比較的聞きやすい英語だと思います。
TAの女性が担当している補足資料のビデオは綺麗な英語で聞きやすいですけれど割と早口です。

剛体力学（剛体の回転とかモーメントとか角運動量とか慣性テンソルとか）が分からない、あるいは苦手な人は先にさらっておくか、力学の教科書を手元に置いての受講をおすすめします。*4。

Week 1: Introduction to Aerial Robotics

1.1 Introduction - 序論

無人航空機 (Unmanned aerial vehicle (UAV))

空中ロボット、遠隔操作航空機 (RPV)、ドローン（などいろいろ言い方はあるが同じものを指している）

クワッドローター（推進に4つの回転翼を用いるドローン）

ロール＆ピッチ、ヨー、並進運動 (translation)

ロール・ピッチ・ヨーって何千回聞いてもどれがどれってパッと言えないですね…ネットで見つけた「ヨーソローはyaw slowから来てる」というガセ情報*5のお陰でyawが垂直軸中心の（水平面内の）回転だというのは分かるようになりましたが。あっちむいてホイ的に言うと左（右）を向くのがyaw、上（下）を向くのがpitchで、rollは首をかしげる動きです。
f:id:n4_t:20180508161917j:plain:h128 f:id:n4_t:20180508161927j:plain:h128 f:id:n4_t:20180508162138j:plain:h128
（左からヨー、ピッチ、ロール）

自律航行の重要な構成要素

状況の推定、制御、地形把握、飛行計画

GPSや外部モーションキャプチャカメラなしでのナビゲーション
SLAM (Simultaneous Localization And Mapping)／ビーコン（カメラで位置を把握するための二次元バーコードみたいな白黒画像）

ドローンの応用分野

精密農場経営、建築、考古学調査、（人間のカメラマンには不可能な位置からの）写真撮影、ファーストレスポンダー（初期対応）ロボット、

Quiz 1.1

他のCourseraのコース同様、Quizで規定のスコアを取ることはプログラミング実習と並んでコース修了の必要条件となっています。満点でなくても修了はできますが分からない問題を残すのは気持ち悪いのでForumで確認しましょう。

〈読み物〉MATLABプログラミング環境のセットアップ

〈読み物〉MATLAB チュートリアル

このコースの参加者にはWebブラウザ上で使えるMATLABの1ヶ月利用権が与えられるのでそれを使います。
（チュートリアルは全然見てないです）

1.2 Energetics and System Design - エネルギー論とシステム設計

基本的な力学（ローターの物理学）

ローターの回転によって生じる推力(thrust) $\mathbf{F}_i=k_Fω_i^2$ (角速度の2乗に比例)
抗力モーメント(drag moment) $\mathbf{M}_i=k_Mω_i^2$ (角速度の2乗に比例) このモーメントはローターの回転の逆向きに生じる
合力 $\mathbf{F}=\mathbf{F}_1+\mathbf{F}_2+\mathbf{F}_3+\mathbf{F}_4-mg\mathbf{a}_3$ （ $a_3$ は垂直方向の軸）
合成モーメント $\mathbf{M}=\mathbf{r}_1\times\mathbf{F}_1+\mathbf{r}_2\times\mathbf{F}_2+\mathbf{r}_3\times\mathbf{F}_3+\mathbf{r}_4\times\mathbf{F}_4+\mathbf{M}_1+\mathbf{M}_2+\mathbf{M}_3+\mathbf{M}_4$
クワッドローターで4つのローターを交互に逆向きに回転させるのは $M_1$ 〜 $M_4$ を打ち消すため。（さもないとz軸中心に回転してしまう）*6

そもそもモーメントって何？なんでベクトルが回転軸の向きなの？という辺りでつまづいたので、小中学校の理科の授業のレベルの理解から理系大学生辺りのレベルまで押し上げるために並行して自習しました。

力学と1次元の線形制御

線形制御(linear control)と言っているのは、roll/pitch/yaw各角度がゼロに近い前提で $\sin θ\sim θ, \cos θ\sim1$ のような置き換えを行い、推力やモーメントを線形代数的に求める方法のこと。

PD制御：位置誤差 $e(t)=x^{des}(t)-x(t)$ に比例する成分Pと、速度誤差 $\dot e(t)$ に比例（＝位置成分の微分に比例）する成分Dを用いた制御。以降のプログラミング演習で用いられるのはPD制御。 $$ u(t)=\mathrm{min}(\ddot x^{des}(t)+K_v\dot e(t)+K_pe(t),u_{max}) $$
PID制御：PDに加え積分成分Iを用いた制御。$$ u(t)=\mathrm{min}(\ddot x^{des}(t)+K_v\dot e(t)+K_pe(t)+K_I\int_0^te(τ)dτ,u_{max}) $$
位置成分の係数 $K_p$ が大きいと行き過ぎてから振動して収束する／ $K_p$ が小さいと下からそっと漸近する
速度成分の係数 $K_v$ が大きいと"overdamped (過減衰)"　cf. 減衰振動 - Wikipedia

設計の考察

最大推力はモーターの最大トルクで制限される。この制約下でどう制御するか。→PD制御、PID制御
推力と電力消費量の関係、バッテリー重量と供給可能電力量の関係
センサやカメラの重量と消費電力

敏捷性・操縦性

敏捷性の最大化：停止距離の最小化
減速なしでの高速ターン
短時間での加速→ $a_max$ (線形加速) を最大化 = $\frac{u_1,max}{W}$ を最大化( $u_1$ は推力の合計)
短時間でのロール／ピッチ→ $α_max$ (角加速) を最大化 = $\frac{u_2,max}{I_xx}$ を最大化( $u_2$ はモーメントの合計)

コンポーネントの選択

各種フレームやモーター、プロペラの寸法、重量、積載量、最大推力
基本ハードウェア

サイズの効果

重量と慣性 $m\sim l^3$ , $I\sim l^5$ (since $r\sim l$ )
推力 $F\sim πr^2\times(ωr)^2$ , $F\sim l^2v^2$ , $a\sim \frac{F}{m}$
モーメント $M\sim Fl$ , $M\sim l^3v^2$ , $α\sim\frac{M}{I}$
最大加速度 $a\sim\frac{v^2}{l}$ , $α\sim\frac{v^2}{l^2}$
スケーリング

　　Froude scaling: $v\sim\sqrt l$ , $F\sim l^3$ ; $a\sim1, α\sim\frac{1}{l}$
　　Mach scaling: $v\sim 1$ , $F\sim l^2$ ; $a\sim\frac{1}{l}, α\sim\frac{1}{l^2}$

力学系 (dynamical system): 作用の効果が直ちには現れない系。状態の時間発展はよく常微分方程式 *7の集合によって与えられる。（質量とバネ、カート上の振り子、クワッドローターを例に挙げ説明）
収束率。誤差をどのくらい速く0に持っていけるか？

　　 $\forall t\gt0 \|e(t)\|\ltαe^{-βt}$ を満たす $α,β,t_0$ があるとき、誤差は指数的に収束する

Quiz 1.2

Quizの設問に、PD制御のシミュレータを用って推力と機体重量の比率が制御のレスポンスにどう影響するか確認させる（パラメータの数値を入力する）問題がありました。rise timeは1秒以内、overshootは5%以内になるようにパラメータを色々いじってみるだけで、さほど難しくはないです。

補足資料

力学系について、収束率のこと

Week 2

2.1 Quadrotor Kinematics - クワッドローターの運動学

剛体変換 (rigid body transformation)

参照系（基準座標系）(reference frame)
剛体変位 (displacement: 位置の変化)
- 長さの保存：剛体の中の2点p, qについて、変位gの前後で $\|g(p)-g(q)\|=\|p-q\|$
- クロス積の保存：剛体の中の3点 $\mathrm{p,q,r}$ とベクトル $v=\overrightarrow{\mathrm{pq}},w=\overrightarrow{\mathrm{pr}}$ について、変位gによるベクトルの変換を $g_*$ とすると $g_*(v)\times g_*(w)=g_*(v\times w)$
- 内積の保存： $g_*(v)\cdot g_*(w)=g_*(v\cdot w)$

回転

回転行列Rの性質：直交、det=+1、積について閉じている（2つの回転行列を掛け合わせたものも回転行列）、Rの逆行列もまた回転行列
x軸回りにθ回転

$$ Rot(x,θ) = \left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos θ & -\sin θ \\
0 & \sin θ & \cos θ
\end{array}\right) $$

y軸回りにθ回転

$$ Rot(y,θ) = \left(\begin{array}{ccc}
\cos θ & 0 & \sin θ \\
0 & 1 & 0 \\
-\sin θ & 0 & \cos θ
\end{array}\right) $$

z軸回りにθ回転

$$ Rot(z,θ) = \left(\begin{array}{ccc}
\cos θ & -\sin θ & 0 \\
\sin θ & \cos θ & 0 \\
0 & 0 & 1
\end{array}\right) $$

特殊直交群 SO(n) : n行n列の直交行列で、行列式が+1のもの。回転行列は SO(3)

$$ SO(3) = {R\in\mathbb{R}^{3\times3}|R^TR=RR^T=I, \det R=1} $$

球面上の座標系：（緯度・経度みたいにパラメトライズ）

オイラー角

任意の回転は線形独立な軸の回りの回転を3つ繋げれば記述できる：
$^AR_D=^AR_B\times^BR_C\times^CR_D$

X-Y-Zオイラー角 $^AR_D=\mathrm{Rot}(x,ψ)\times\mathrm{Rot}(y,φ)\times\mathrm{Rot}(z,θ)$ (roll × pitch × yaw)
Z-Y-Zオイラー角 $^AR_D=\mathrm{Rot}(z,φ)\times\mathrm{Rot}(y,θ)\times\mathrm{Rot}(z,ψ)$

$$ R = \left[\begin{array}{ccc}
\cos φ\cos θ\cos ψ-\sin φ\sin ψ & -\cos φ\cos θ\sin ψ - \sin φ\cos ψ & \cos φ\sin θ \\
\sin φ\cos θ\cos ψ-\cos φ\sin ψ & -\sin φ\cos θ\sin ψ - \cos φ\cos ψ & \sin φ\sin θ \\
-\sin θ\cos ψ & \sin θ\sin ψ & \cos θ
\end{array}\right] $$

$θ=\pm\cos^{-1}(R_{33})$
$ψ=\mathrm{atan2}(\frac{R_{32}}{\sin θ},\frac{-R_{31}}{\sin θ})$
$φ=\mathrm{atan2}(\frac{R_{23}}{\sin θ},\frac{R_{13}}{\sin θ})$

※ $R_{33}=\pm1$ の場合、残りがφ+ψの関数になる（φ,ψが一意に定まらない）

（剛体回転における）オイラーの定理：剛体中の1点（Oとする）の位置が変わらない任意の剛体の変位は、点Oを通る固定の軸の回りの回転と等価である*8
回転軸u(単位ベクトル)と、その回りを回ろうとしている点p（単位ベクトル）があるとする
- pのuと平行な成分= $(\mathbf{p}.\mathbf{u})\mathbf{u}$
- pのuと垂直な成分= $\mathbf{p}-(\mathbf{p}.\mathbf{u})\mathbf{u}$ （この向きにv、さらにu,vと垂直な方向に $\mathbf{w}(=\mathbf{u}\times\mathbf{v})$ を取る）
軸uを中心にpがφだけ回転することを考える。
- uと平行な成分は不変 → $(\mathbf{p}.\mathbf{u})\mathbf{u}$
- uと垂直な成分は… vが $\mathbf{v}\cos φ+\mathbf{w}\sin φ$ に移るので → $(\mathbf{p}-(\mathbf{p}.\mathbf{u})\mathbf{u})\cos φ+\mathbf{u}\times(\mathbf{p}-(\mathbf{p}.\mathbf{u})\mathbf{u})\sin φ$
- 合計すると $\mathbf{p}cos φ + \mathbf{uu}^T(1-\cos φ)\mathbf{p}+\mathbf{u}\times\mathbf{p}\sin φ$

ところで、
$$ \mathbf{a}\times\mathbf{b} = \left[\begin{array}{c}
a_1 \\
a_2 \\
a_3
\end{array}\right] \times \left[\begin{array}{c}
b_1 \\
b_2 \\
b_3
\end{array}\right] = \left[\begin{array}{c}
a_2b_3 - a_3b_2 \\
a_3b_1 - a_1b_3 \\
a_1b_2 - a_2b_1
\end{array}\right] = \left[\begin{array}{ccc}
0 & -a_3 & a_2 \\
a_3 & 0 & -a_1 \\
-a_2 & a_1 & 0
\end{array}\right]\left[\begin{array}{c}
b_1 \\
b_2 \\
b_3
\end{array}\right] $$
から、3×3の歪対称行列(skew-symmetric matrix) $$\left[\begin{array}{ccc}
0 & -a_3 & a_2 \\
a_3 & 0 & -a_1 \\
-a_2 & a_1 & 0
\end{array}\right] $$ が $\mathbf{a}\times$ と等価であることがわかる。これを $\hat{\mathbf{a}}$ と書き、線形演算子（hat演算子）として用いることにする。
$$ \hat{\mathbf{a}}\mathbf{b} = \mathbf{a}\times\mathbf{b} $$

回転の軸/角度表現

先程の $\mathbf{p}cos φ + \mathbf{uu}^T(1-\cos φ)\mathbf{p}+\mathbf{u}\times\mathbf{p}\sin φ$ をhat演算子を用いて書くと $$ \mathbf{p}cos φ + \mathbf{uu}^T(1-\cos φ)\mathbf{p}+\hat{\mathbf{u}}\mathbf{p}\sin φ $$ となる。一般にベクトルpを、単位ベクトルuを軸として角度φ (rad)だけ回転させると $Rp=p\cos φ + uu^T(1-\cos φ)p+\hat{u}p\sin φ$ となり、この回転を表す回転行列Rは
$$ R=Rot(u,φ)=I\cos φ + uu^T(1-\cos φ)+\hat{u}\sin φ $$
で表すことができる（Rodriguesの公式）。

同じ回転を表す (回転軸u, 回転角度φ) の組み合わせは無数にある。角度を [0, π] の範囲に制限すれば1-1対応になるが、φ=0のとき軸は定まらないし、φ=πのとき軸の向きが逆でも同じ結果になるという例外がある。

回転と角速度

回転行列の時間微分

$R^T(t)R(t)=I, R(t)R^T(t)=I$ → $\dot{R}^TR+R^T\dot{R}=0, \dot{R}R^T+R\dot{R}^T=0$
$R^T\dot{R}$ と $\dot{R}R^T$ は歪対称行列。

飛行するクワッドローター上のある1点 p があるとする。これは body-fixed frame（剛体系：地上の慣性系とは切り離された、飛行体固定の座標系）では定ベクトル。
body-fixed frame の座標を inertial frame（慣性系）の座標に翻訳する回転行列を R(t) とする。これは時刻tの関数。
点p の慣性系での座標q(t)は $q(t)=R(t)p$ 。剛体が回転すれば変動するので時刻tの関数。
qを（tで）微分すると。pは定ベクトルなので微分すると消える。
- $\dot{q}$ は慣性系から見た点pの速度。
両辺に $R^T$ を掛ける（＝慣性系座標を剛体系座標に変換する回転）と… $R^T\dot{q}=R^T\dot{R}p$ が得られる。これは剛体系から見た点の速度。右辺の $R^T\dot{R}$ は先述の歪対称行列で、剛体系における角速度 $\hat{ω}^b$ をエンコードしている。
また、 $\dot{q}=\dot{R}p=\dot{R}(R^TR)p=\dot{R}R^T(Rp)=\dot{R}R^Tq$ が導ける。 $\dot{q}$ は慣性系における点の速度。右辺の $\dot{R}R^T$ は慣性系における角速度 $\hat{ω}^s$ をエンコードしている。

Quiz 2.1

2.2 Quadrotor Kinematics - 補足資料

剛体の移動、MATLABのsymbolic calculations、atan2関数の使い方、行列の固有値と固有ベクトル、クォータニオン（四元数）を用いた回転の表現、行列の微分、歪対称行列とhat (^) 演算子
剛体の変位(displacement)は、回転を表す行列Rと平行移動（並進運動:translation）ベクトルdで記述できる。 $q'=Rq+d$
atan2(y,x)は競プロでもよく使うしお馴染みの関数。xとyの両方を指定することで象限を1つに絞ることができる。

determinant

2x2行列 A=[a b;c d] について det(A)=ad-bc だけどこれは2つのベクトル(a,b),(c,d)を2辺とする平行四辺形(parallelogram)の面積に等しい。
3x3行列 A=[a b c;d e f;g h i] でも似たようなことが言えて、det(A)=aei+bfg+cdh-ceg-bdi-afh は3つのベクトル(a,b,c),(d,e,f),(g,h,i)を3辺とする平行六面体(parallelepiped)の体積に等しい。

2.3 Quadrotor Dynamics - クワッドローターの力学

（剛体の回転運動まわりの力学の知識がなかったので、一旦足を止めて自習しました）

慣性主軸と主慣性モーメント Principal Axes and Principal Moments of Inertia

慣性テンソル行列I
$$ I= \left(\begin{array}{ccc}
I_{xx} & I_{xy} & I_{xz} \\
I_{yx} & I_{yy} & I_{yz} \\
I_{zx} & I_{zy} & I_{zz}
\end{array}\right) $$
は、適当な直交座標系 ${e_1,e_2,e_3}$ を選んで対角化することができる。
この時の座標軸 $e_1,e_2,e_3$ が慣性主軸で、慣性モーメント（対角行列の対角成分 $I_1,I_2,I_3$ ）が主慣性モーメントと呼ばれる。角運動量を
$$ R = \left(\begin{array}{c}
L_1 \\
L_2 \\
L_3
\end{array}\right) = \left(\begin{array}{ccc}
I_1 & 0 & 0 \\
0 & I_2 & 0 \\
0 & 0 & I_3
\end{array}\right) \left(\begin{array}{c}
ω_1 \\
ω_2 \\
ω_3
\end{array}\right) $$
と表すことが出来て便利。

ニュートン=オイラー方程式

線形運動量の変化率について $\mathbf{F}=\frac{{}^Ad\mathbf{L}}{dt}$ は剛体でも成り立つ
角運動量Hはinertia Iと角速度ωの積で表せる $^A\mathbf{H}^S_c=\mathbf{I}_c\cdot^Aω^B$ 。（運動量=質量×速度、に対応している）
オイラーの方程式：角運動量の微分dH/dt＝外力からのモーメント総量M
- これは慣性系Aでの計算
これを剛体系に直すとになるらしい
- $\mathbf{b}_1,\mathbf{b}_2,\mathbf{b}_3$ が慣性主軸に沿っていて、慣性系での角速度は $^Aω^B=ω_1\mathbf{b}_1+ω_2\mathbf{b}_2+ω_3\mathbf{b}_3$ と表せる
- モーメント総量の式の左辺は慣性系Aでの $H_C$ の微分で、慣性系における角速度 $ω^s$ を用いて

$\dot{q}=\dot{R}R^Tq=\hat{ω}^sq$ と置き換えられるので
$\frac{^Ad{}^A\mathbf{H}^S_C}{dt}=\hat{ω}^s\mathbf{H}^S_C=^A\hat{ω}^B\mathbf{H}^S_C$ …あれ？ $\frac{^Bd{}^A\mathbf{H}_C}{dt}$ が足りない。（ここの導出は飛ばそう。）

$\frac{^Bd{}^A\mathbf{H}_C}{dt}=\frac{d}{dt}\mathbf{I}_c\cdot^Aω^B=\mathbf{I}_c\cdot^A\dot{ω}^B=I_{11}\dot{ω}_1\mathbf{b}_1+I_{22}\dot{ω}_2\mathbf{b}_2+I_{33}\dot{ω}_3\mathbf{b}_3$
$\mathbf{H}_C=\mathbf{I}ω$ も合わせて

$$ \mathbf{I}\dot{ω}+\hat{ω}\mathbf{I}ω=\mathbf{M} $$
成分を書くと
$$ I= \left[\begin{array}{ccc}
I_{11} & 0 & 0 \\
0 & I_{22} & 0 \\
0 & 0 & I_{33}
\end{array}\right] \left[\begin{array}{c}
\dot{ω}_1 \\
\dot{ω}_2 \\
\dot{ω}_3
\end{array}\right] + \left[\begin{array}{ccc}
0 & -ω_3 & ω_2 \\
ω_3 & 0 & -ω_1 \\
-ω_2 & ω_1 & 0
\end{array}\right] + \left[\begin{array}{ccc}
I_{11} & 0 & 0 \\
0 & I_{22} & 0 \\
0 & 0 & I_{33}
\end{array}\right] \left[\begin{array}{c}
ω_1 =p \\
ω_2 =q \\
ω_3 = r
\end{array}\right] = \left[\begin{array}{c}
M_{C,1} \\
M_{C,2} \\
M_{C,3}
\end{array}\right] $$

クワッドローターの運動方程式

各ローターの推力 $F_i=k_Fω^2_i$ 、ーメント $M_i=k_Mω^2_i$
合力 $\mathbf{F}=\mathbf{F}_1+\mathbf{F}_2+\mathbf{F}_3+\mathbf{F}_4-mg\mathbf{a}_3$
合成モーメント $\mathbf{M}=\mathbf{r}_1\times\mathbf{F}_1+\mathbf{r}_2\times\mathbf{F}_2+\mathbf{r}_3\times\mathbf{F}_3+\mathbf{r}_4\times\mathbf{F}_4+\mathbf{M}_1+\mathbf{M}_2+\mathbf{M}_3+\mathbf{M}_4$

ニュートンの運動方程式

$$ \mathbf{F}=m\mathbf{a}=m\ddot{\mathbf{r}} = \left[\begin{array}{c}
0 \\
0 \\
-mg
\end{array}\right] + R \left[\begin{array}{c}
0 \\
0 \\
F_1+F_2+F_3+F_4
\end{array}\right] $$

オイラーの方程式

$$ I \left[\begin{array}{c}
\dot{p} \\
\dot{q} \\
\dot{r}
\end{array}\right] = \left[\begin{array}{c}
L(F_2-F_4) \\
L(F_3-F_1) \\
M_1-M_2+M_3-M_4
\end{array}\right] - \left[\begin{array}{c}
p \\
q \\
r
\end{array}\right] \times I \left[\begin{array}{c}
p \\
q \\
r
\end{array}\right] $$

推力 $F_1+F_2+F_3+F_4$ を $u_1$
合成モーメント（オイラー方程式の右辺第1項）を $u_2$ とする
角速度 (p,q,r) はロール・ピッチ・ヨー (φ,θ,ψ) の時間微分を剛体系座標に回転したもの

$$ \left[\begin{array}{c}
p \\
q \\
r
\end{array}\right] = \left[\begin{array}{ccc}
\cos θ & 0 & -\cos φ\sin θ \\
0 & 1 & \sin φ \\
\sin θ & 0 & \cos φ\cos θ
\end{array}\right] \left[\begin{array}{c}
\dot{φ} \\
\dot{θ} \\
\dot{ψ}
\end{array}\right] $$

プログラミング課題: 1-D Quadrotor Control

移動をz軸（上下）方向に制約した条件下でクワッドローターを制御するのに必要な出力を、現在位置・現在速度・目標位置・目標速度（あと重力加速度とクワッドローターの重量）を引数に求める関数を書く。（MATLAB）
課題の提出は、MATLAB上で採点プログラム submit.m を実行して得られる謎の出力 *.mat をCourseraの宿題ページのフォームにアップロードするという方式になっている。

補足資料:state-space form

状態ベクトル：
$$ q=[x,y,z,φ,θ,ψ]^T, x=[q, \dot{q}] $$

q: 系のconfiguration (position)を記述する
x: 系の状態(state)を記述する]

これを用いて常微分方程式(ordinary differential equasions)を記述する。 $\dot{\mathbf{x}}=f(\mathbf{x},u)$

Week 3

3.1 制御

2次元（y-z軸）でのクワッドローター制御

クワッドローターの運動の方向を2次元平面（y-z軸）上に制約したモデルで考える。
角度パラメータはφ1つだけ（平衡状態にある時にはφ=0）。

運動方程式の線形化

// state-space form
運動方程式は非線形（これを線形化したい）
空中で静止平衡状態(equilibrium hover)を保つ場合 $y_0,z_0,φ_0=0, u_{1,0}=mg,u_{2,0}=0$ なのでこれを利用する。

軌道の追跡

ある時点（時刻t）にいるべき座標、速度、加速度が与えられている。
実際の座標、速度、加速度との誤差から、必要な加速度 $\ddot{\mathbf{r}}_c$ を求めたい。

ネスト状の制御構造（姿勢コントローラに入った剛体系からのフィードバックが必要なモーメント u_1 が求められ、位置コントローラに入ったフィードバックから必要な推力 u_2 が求められる）

3次元（x-y-z軸）でのクワッドローター制御

角度パラメータは3つ（ロール・ピッチ・ヨー）に増える。
軌道追跡では位置・速度・加速度に加え、ヨー（水平回転角）成分とその1階・2階微分までが求められる。
ニュートン・オイラー方程式を解いて必要な推力u_1とモーメントu_2を得る。

プログラミング課題: 2-D Quadrotor Control

3.2 経路計画

時間・運行・軌道

スムーズな3次元軌道

スタートとゴールの位置
経由地(waypoints)の位置
スムーズさの基準（一般に入力の変化率の最小化に置き換えられる）
系のorder n（n-1階微分までの境界条件がある）

変分法 (calculus of variations)

$$ x^*(t) = \mathrm{arg~min}_{x(t)}\int_0^T\mathcal{L}(\dot{x},x,t)dt $$
オイラー・ラグランジュ方程式
$$ \frac{d}{dt}(\frac{\partial\mathcal{L}}{\partial\dot{x}})-\frac{\partial\mathcal{L}}{\partial x}=0 $$
というか
$$ \frac{\partial\mathcal{L}}{\partial x}-\frac{d}{dt}(\frac{\partial\mathcal{L}}{\partial\dot{x}})=0 $$

スムーズな軌道 (n=1, n=2, n≧3)

$$ x^*(t) = \mathrm{arg~min}_{x(t)}\int_0^T(x^{(n)})^2dt $$

n=1: 最短距離 (最小速度）
n=2: 最小加速度
n=3: 最小加加速度(jerk)
n=4: 最小加加加速度(snap)

オイラー・ラグランジュ方程式（n階）

$$ \frac{\partial\mathcal{L}}{\partial x}
- \frac{d}{dt}(\frac{\partial\mathcal{L}}{\partial\dot{x}})
+ \frac{d^2}{dt^2}(\frac{\partial\mathcal{L}}{\partial\ddot{x}})
+ ... + (-1)^n\frac{d^n}{dt^n}(\frac{\partial\mathcal{L}}{\partial x^{(n)}})=0 $$

最小ジャーク軌道の場合、xの6階微分がゼロ→5次方程式
求めるべき係数は6つ。6つの制約条件（t=0およびt=Tにおける位置・速度・加速度の値）から求まる。

多次元への拡張が可能（xだけでなくy,z,..を加えることができる）
二次元平面系での最小ジャーク軌道
スムーズな軌道

（x軸のみの場合から）
経由すべき点（m+1個）が
$$ t=[t_0,t_1,t_2,...,t_m]^T, x=[x_0,x_1,x_2,...,x_m]^T $$
で与えられている。これはm個の区間に分割して考える。
それぞれを直線で結んでしまうと、連続ではあるが微分不可能な軌道になる。（力学系として微分方程式で解くことができない）
二次の系で最小加速度軌道（曲線）を考える。

3次スプライン曲線

各区間が3次方程式（それぞれ4個の係数がつくので求めるには計4m個の制約が必要）

区間の始点と終点の位置による制約（2m個）
区間の継ぎ目（＝経由点）で1階微分・2階微分が等しいという制約（2(m-1)個）
始点と終点で位置の1階微分が0（初速と終速が0）という制約（2個）

同じようにn次のスプライン曲線を考えることができる。各区間がn次方程式でn+1個ずつの係数がつくので、求めるにはm(n+1)個の制約が必要。

クワッドローターの経路計画

現在の位置・速度・角度・角速度などの情報からニュートン・オイラー方程式のu_1,u_2を求める制御ループ
- 内側のループ（姿勢制御系）→必要なモーメントu_2を求める
- 外側のループ（位置制御系）→必要な推力u_1を求める
最小スナップ（加加加速度）軌道

位置制御系は4次の系（線形化による近似の式をごにょごにょしていくと示せる）なので、4階微分可能な系であることが求められる

軌道の自動合成
空中で物を掴んだり操作したりする
perching (止まり木に止まる)
最小スナップ軌道を求める制約条件
障害物（凸包多面体モデル）

衝突判定：障害物のポリゴン面の法線とドローンの位置ベクトルの内積が一定値以下（＝ある平面より上か下か、というか物体から見て外側か内側かを判定している）だとNG

荷物をぶら下げて運ぶ（ぶら下げている紐の長さより直径の小さいリングを、荷物がとる（ドローンから見たら振り子のような）軌道も加味しつつくぐり抜けている

補足資料

最小速度軌道、オイラー=ラグランジュ方程式による最小速度軌道、最小加加速度*9軌道の係数を求める、クワッドローターの運動方程式の線形化

Quiz 3

Week 4

オンボードでの状態推定、非線形制御、群れ(swarm)

センシングと状態推定

ドローン機体上に搭載したセンサを用いた（部屋に設置したカメラ等には頼らない）状態推定

センサ：GPS、レーザースキャナ、気圧高度計、ステレオカメラ、下方カメラ、IMU（慣性計測ユニット）
センサ情報を利用した各種推定器：レーザ走行距離計測器、高度推定器、視覚走行距離計測器、速度推定器
センサ情報は地図情報の精細化にも用いられる
各種推定器の出力がマルチセンサ無香(unscented)カルマンフィルタに集められる。（カルマンフィルタってPRMLで聞いたことがあるぞ。無香って何だ→カルマンフィルタについて - こうきょの日記）
カルマンフィルタ（と位置情報）からPose Graph SLAMへ
SLAM+地図情報→経路計画器→軌道生成器→推力・モーメント制御器

システム設計で考慮すべき点

大きい機体はより良いセンサやプロセッサを積めるので多くのことが出来る
- バッテリも大きいものを積めるので航続時間が伸び、長い時間のミッションが可能になる
小さい機体は制約のきつい環境でも航行可能
- 敏捷性・操作性ともに小さいものが大きなものに勝る

非線形制御

線形制御の制約：ロール・ピッチ角と速度がゼロに近いことを仮定している（ので高速飛行や大きな角度をつけた飛行が制御できない）
推力を向けたい方向のベクトルから回転行列を求め、モーメントに加味する
- 回転行列の誤差は引き算ではなく、 $ΔR=R^TR_{des}$ で求める。回転の角度と軸は前述のRodriguesの公式から求める。

Large basin of attraction

角度誤差の上限はinertiaテンソルの最大固有値に反比例するので、機体が小さければ小さいほど（衝突などによる）大きな角度変動からのリカバリが効くようになる。
（概ねサイズの2.5乗に反比例する）
小さいほうが安全で、より操作性が高まる。

連続制御（空中静止時の線形制御、姿勢のみの制御、非線形制御の間の遷移）
Differential Flatness, Diffeomorphism（微分同相写像 (=differentiable homeomorphism)）

位置(flat output)とそのk階微分成分、は状態（位置や角度とその微分）と入力（u1,u2）から算出できるし、その逆も可能であるという話→微分方程式から求めた最小スナップ軌道がクワッドローターの力学系で有効であることを保証する

複数のロボットの制御

Swarm（群れ）で活動するロボット

1匹では運ぶことのできない大きな物を集団で運ぶ蟻の話

集団で行動する組織の3原則

1. 各個体は独立して行動する
2. 行動は現地の情報に基づく
3. 協力における匿名性（誰が誰でもかまわない）

complexity

ロボットがn台、障害物がm個あるとして

状態空間の次元数：O(n)
潜在的インタラクション数：O(mn+n^2)
- 近隣のロボットとの間に発生するやりとりO(n^2) + 近隣の障害物との間に発生するやりとりO(mn)
各ロボットをゴール位置にアサインする組み合わせ：O(n!)

但し、ゴールアサインについては、個別に最適コースをとらせるだけでは衝突の危険性があるので、各個体間の距離が一定値以上になるように推移させる必要がある。
4つのキーアイデア

ゴールと軌道を並行してアサインする
- アサインメントと軌道計画の並列実行 (CAPT: Concurrent Assignment and Planning of Trajectories) による方法: 複数台分のstateを1つの行列にまとめて制約条件下で最適解を求める
- 〈比較〉n台×ゴールn箇所の間の経路を総当たりで調べた上で、割当問題をハンガリアンアルゴリズムで解く方法
リーダーとフォロワーのネットワーク（絶対的な位置を把握しているリーダーが1台または複数台存在）
匿名性
情報共有

Quiz 4

プログラミング課題: 3-D Quadrotor Control

(1) 直線軌道 (10点)

f:id:n4_t:20180508152330g:plain
f:id:n4_t:20180508150442p:plain:w300 f:id:n4_t:20180508150502p:plain:w300

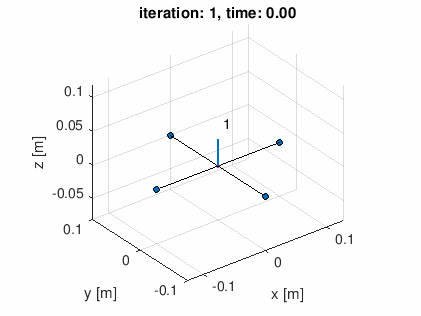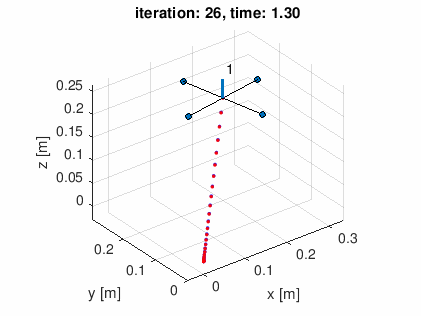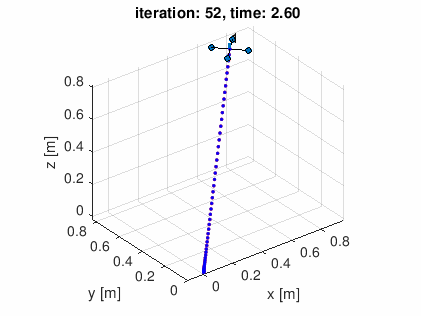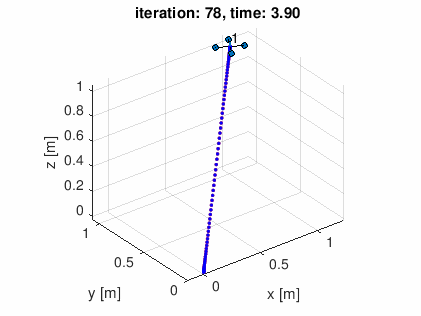
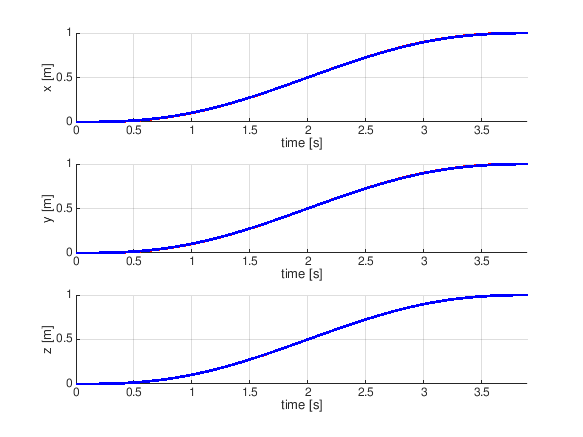
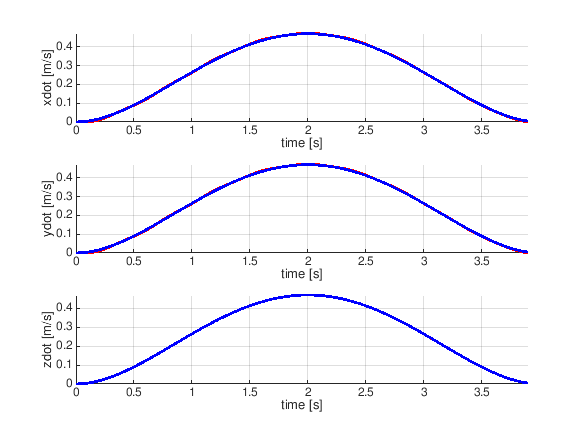
(2) 螺旋状軌道 (20点)

f:id:n4_t:20180508152429g:plain
f:id:n4_t:20180508150617p:plain:w300 f:id:n4_t:20180508150813p:plain:w300

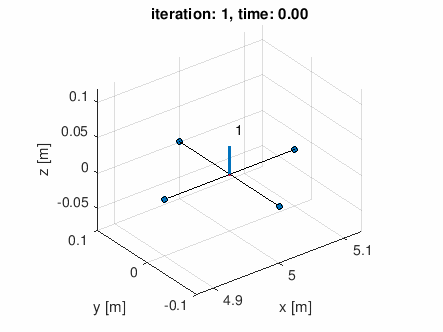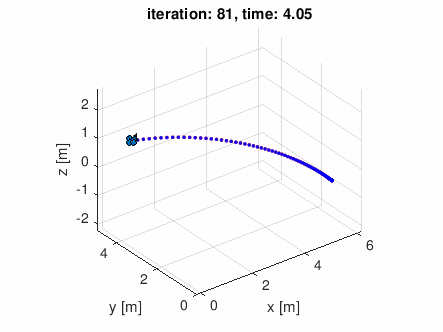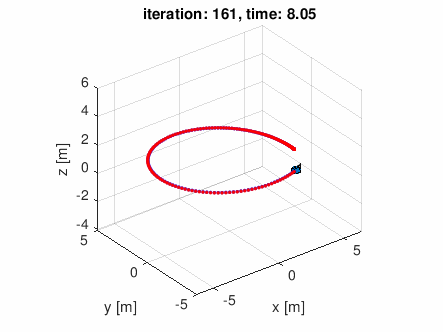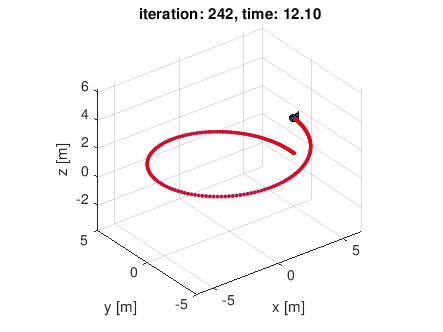
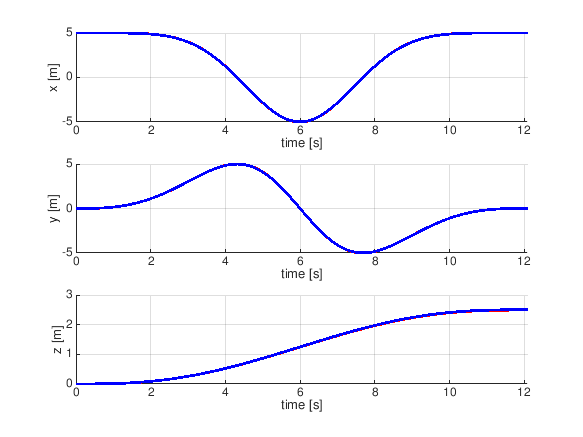
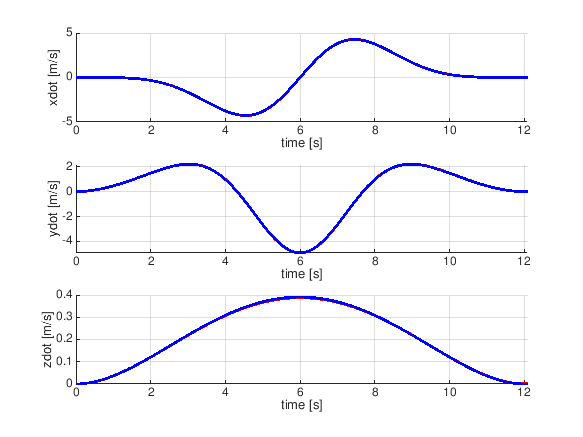
(3) 軌道生成 (20点)

経由すべき地点(waypoints)の座標リストを与えられる。（始点・終点も入れて5ヵ所）

waypoints = [0    0   0;
             1    1   1;
             2    0   2;
             3    -1  1;
             4    0   0]';

Forumを見ると「MATLABのspline関数を使えば行ける」という情報が流れているのだけれど
終点位置での完全停止がうまく行かなくて断念。（速度・加速度は+εの値を取って計算）
教えられた通りに最小スナップ軌道（7次スプライン曲線）を計算した。
シミュレータがt=∞とか投げてきて対応できずに異常終了していた事に気づかず半日潰した。
あと時間微分する際に1/Ti(=du/dt)倍してやらないといけないのを忘れていて、進むべき軌道を2倍ぐらいに拡大したようなコースを辿っていたりとか。
最後は綺麗に止まって
f:id:n4_t:20180508215907p:plain
課題修了。
submit.mが出力する謎ファイルを提出したらすぐに修了通知が来て、Certificateが発行されました。（日本時間で5/8の朝）

f:id:n4_t:20180508152604g:plain f:id:n4_t:20180508152707g:plain
f:id:n4_t:20180508144814p:plain:w300 f:id:n4_t:20180508144807p:plain:w300

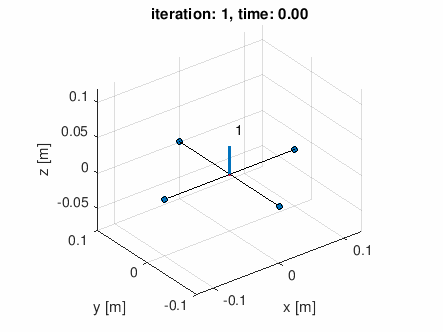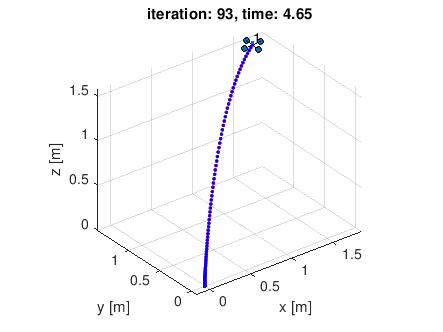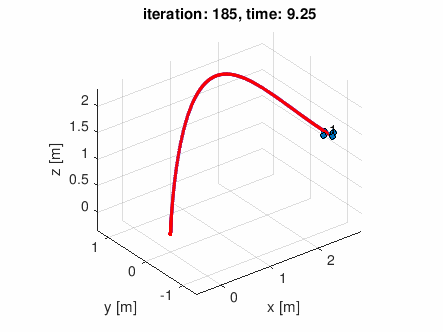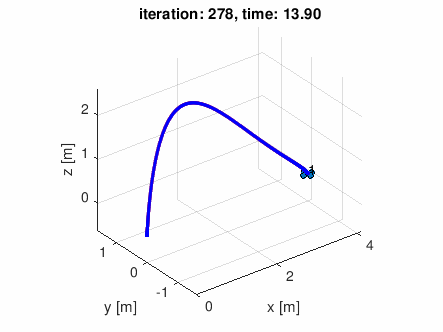
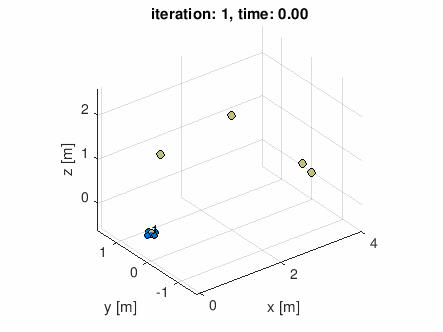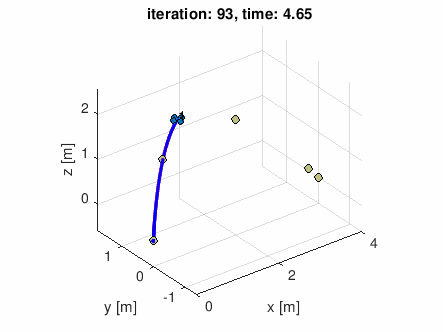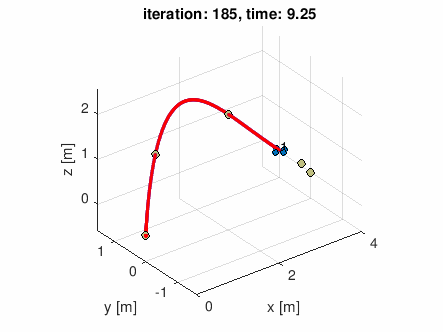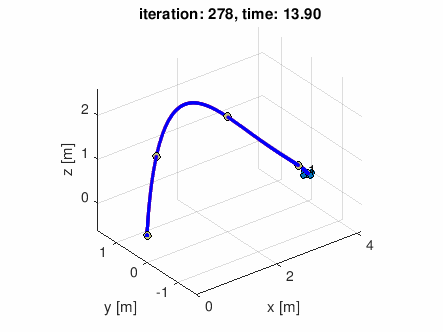
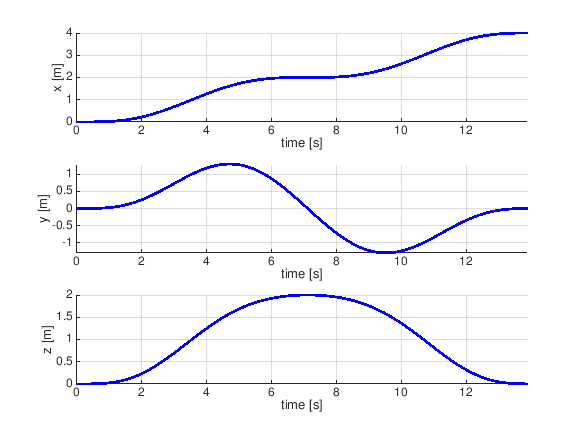
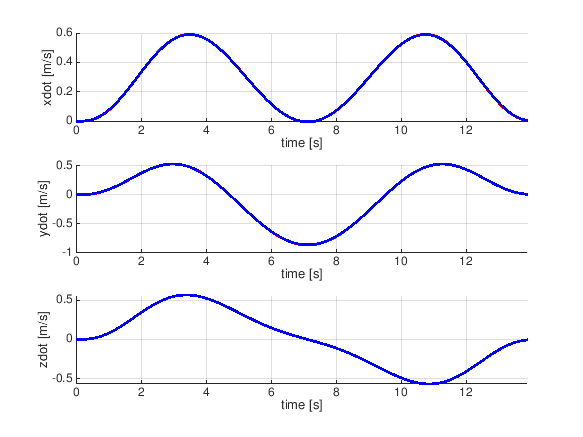
自分で適当な通過点データを作って食わせてみた

waypoints = [-0.5 0   0;
              1   0   0.5;
              1   1   1;
             -0.5 1   1.5;
              1   0   2;
              1   1   2.5;
              0   1   3;
              1  -1  -1;
             -1  -1  -0.5 ]';

f:id:n4_t:20180508152834g:plain f:id:n4_t:20180508152927g:plain
f:id:n4_t:20180508144958p:plain:w300 f:id:n4_t:20180508144951p:plain:w300

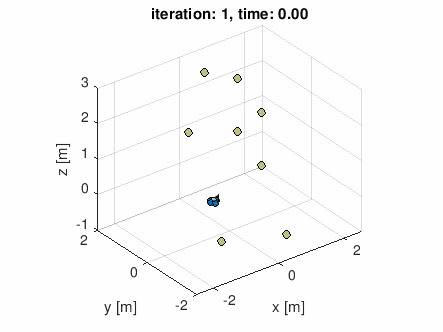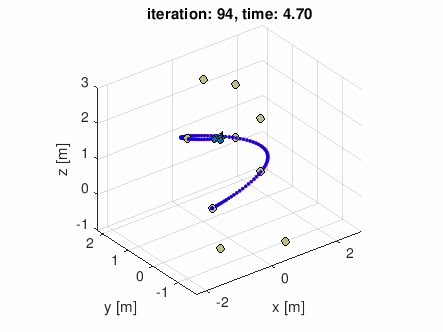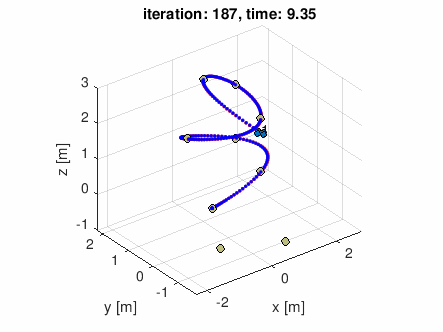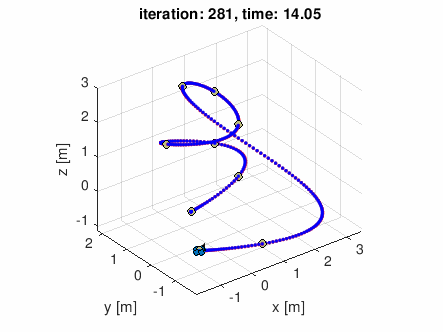
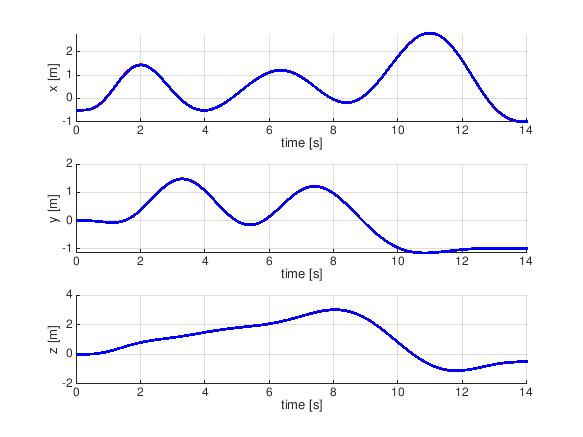
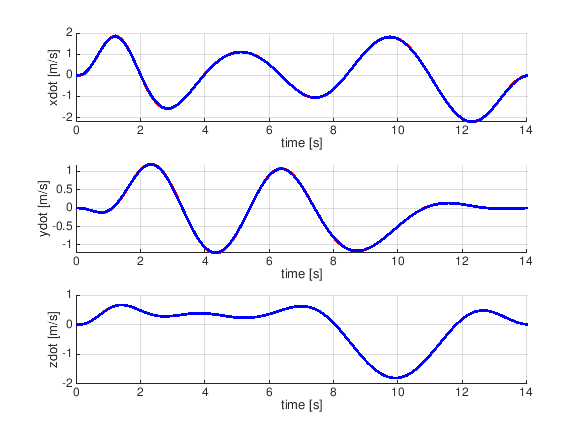
とりあえず修了の報告のためエントリを上げました。
TeX記法の入力が面倒くさいので書きたいところしか書いてないけどもう少し加筆する予定です。(5/8)

*1:下のGIFアニメーションは最終週の課題で実装したプログラムに適当なコース（通過したい空中の点のリスト）を与えてみたシミュレーション結果です((GIFアニメを吐き出すようにシミュレータを若干改造しました。

*2:以前Andrew Ng先生の機械学習の講義でOctaveを触ったことがあるのでなんとなくそんな感じかなと思って臨みました。でも課題であらかじめ与えられるプログラムファイルは手元のOctaveで動かせるかと思ったら動きませんでした。

*3:期限に間に合わなくて次月に繰越になってもまたもらえます

*4:物理学・力学については高校物理レベル+α の知識、具体的にはセンター試験の物理は満点取ったけど大学では力学とか電磁気学の授業をちょっと覗いただけで単位は取ってないはず…ぐらいの知識で講義に臨んでの感想です。

*5:本当にガセです。「宜候」という日本語で、LGTM(looks good to me)的な意味です。

*6:講義ビデオ中の4択とかQuiz 1.2とかで4つのローターの回転が全て同じ方向ではないのがなぜかと聞かれるんだけど、講義ビデオの中では理由の説明はしてないよね？Forumにはあった：https://www.coursera.org/learn/robotics-flight/discussions/forums/JKfF47ldEeWGphLhfbPAyQ/threads/EK7HMNlXEeWU5gr3hvdX9Q 各ローターの回転軸を中心としたdrag momentが本体に影響を及ぼすというのは自明なのだろうか（その辺りの感覚がつかめてない）

*7:ordinary differential equation, ODE

*8:行列Rでp自身に写されるpがある( $\mathbf{p}=R\mathbf{p}$ )、ということは $R\mathbf{p}=λ\mathbf{p}$ は解の1つにλ=1を持つ（＝固有値の1つは1であり、λ=1の固有ベクトルはpである）。

*9:ジャーク(jerk)：加速度の変化率。

Week 1: Introduction to Aerial Robotics

1.1 Introduction - 序論

無人航空機 (Unmanned aerial vehicle (UAV))

クワッドローター（推進に4つの回転翼を用いるドローン）

自律航行の重要な構成要素

状況の推定、制御、地形把握、飛行計画

ドローンの応用分野

Quiz 1.1

〈読み物〉MATLABプログラミング環境のセットアップ

〈読み物〉MATLABチュートリアル

1.2 Energetics and System Design - エネルギー論とシステム設計

基本的な力学（ローターの物理学）

力学と1次元の線形制御

設計の考察

敏捷性・操縦性

コンポーネントの選択

サイズの効果

Quiz 1.2

補足資料

Week 2

2.1 Quadrotor Kinematics - クワッドローターの運動学

剛体変換 (rigid body transformation)

回転

オイラー角

回転の軸/角度表現

回転と角速度

Quiz 2.1

2.2 Quadrotor Kinematics - 補足資料

determinant

2.3 Quadrotor Dynamics - クワッドローターの力学

慣性主軸と主慣性モーメント Principal Axes and Principal Moments of Inertia

ニュートン=オイラー方程式

クワッドローターの運動方程式

プログラミング課題: 1-D Quadrotor Control

補足資料:state-space form

Week 3

3.1 制御

2次元（y-z軸）でのクワッドローター制御

3次元（x-y-z軸）でのクワッドローター制御

プログラミング課題: 2-D Quadrotor Control

3.2 経路計画

時間・運行・軌道

変分法 (calculus of variations)

3次スプライン曲線

クワッドローターの経路計画

補足資料

Quiz 3

Week 4

オンボードでの状態推定、非線形制御、群れ(swarm)

センシングと状態推定

システム設計で考慮すべき点

非線形制御

Large basin of attraction

複数のロボットの制御

complexity

Quiz 4

プログラミング課題: 3-D Quadrotor Control

〈読み物〉MATLAB チュートリアル